题目内容
7.已知公差不为零的等差数列{an},若a1=1,且a1,a2,a5成等比数列.(1)求数列{an}的通项公式;
(2)设bn=2n,求数列{an+bn}的前n项和Sn.
分析 (1)通过a2=1+d、a5=1+4d,利用a1,a2,a5成等比数列计算可知公差d=2,进而可得结论;
(2)分别利用等差数列、等比数列的求和公式计算,相加即可.
解答 解:(1)依题意可知,a2=1+d,a5=1+4d,
∵a1,a2,a5成等比数列,
∴(1+d)2=1+4d,即d2=2d,
解得:d=2或d=0(舍),
∴an=1+2(n-1)=2n-1;
(2)由(1)可知等差数列{an}的前n项和Pn=$\frac{n(1+2n-1)}{2}$=n2,
∵bn=2n,
∴数列{bn}的前n项和Qn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2,
∴Sn=n2+2n+1-2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.若关于x的方程(log2x)2+2alog2x+1=0有大于1的实数解,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | (1,+∞) | D. | (-∞,-1]∪[1,+∞) |
15.不等式2+log0.5(5-x)+log2$\frac{1}{x}$>0的解集是( )
| A. | (0,+∞) | B. | (-∞,5) | C. | (0,1)∪(4,5) | D. | 空集 |
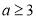 ,函数
,函数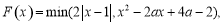 其中
其中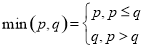 .
.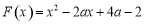 成立的
成立的 的取值范围;
的取值范围;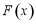 的最小值
的最小值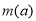 ;
;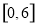 上的最大值
上的最大值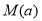 .
. ,且
,且 为第四象限角,则
为第四象限角,则 的值等于
的值等于 B.
B. C.
C. D.
D.