题目内容
设单位向量 、
、 夹角是60°,
夹角是60°, ,
, 若
若 、
、 夹角为锐角,则实数t的取值范围是________.
夹角为锐角,则实数t的取值范围是________.
t>-1 且t≠1
分析:首先根据条件计算出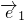 •
•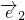 =
= ,再利用向量积的运算求出
,再利用向量积的运算求出 的值,进而根据题中的条件得到
的值,进而根据题中的条件得到 =
= (t+1)>0,并且
(t+1)>0,并且 ,即可求出答案.
,即可求出答案.
解答:由题意可得: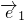 2=1,
2=1,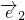 2=1,
2=1,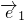 •
•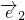 =1×1×cos60°=
=1×1×cos60°= ,
,
因为 ,
, ,
,
所以 =(
=(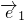 +
+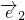 )•(
)•(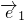 +t
+t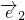 )=
)=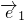 2+(t+1)
2+(t+1)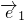 •
•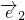 +t
+t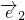 2=
2= (t+1).
(t+1).
因为 、
、 夹角为锐角,
夹角为锐角,
所以 =
= (t+1)>0,并且
(t+1)>0,并且 ,
,
所以解得:t>-1 且t≠1.
故答案为:t>-1 且t≠1.
点评:本题主要考查向量的数量积运算,以及利用向量的数量积解决向量的夹角问题,一定注意共线的情况.
分析:首先根据条件计算出
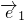 •
•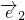 =
= ,再利用向量积的运算求出
,再利用向量积的运算求出 的值,进而根据题中的条件得到
的值,进而根据题中的条件得到 =
= (t+1)>0,并且
(t+1)>0,并且 ,即可求出答案.
,即可求出答案.解答:由题意可得:
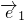 2=1,
2=1,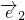 2=1,
2=1,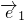 •
•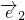 =1×1×cos60°=
=1×1×cos60°= ,
,因为
 ,
, ,
,所以
 =(
=(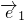 +
+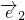 )•(
)•(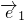 +t
+t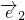 )=
)=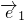 2+(t+1)
2+(t+1)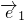 •
•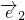 +t
+t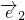 2=
2= (t+1).
(t+1).因为
 、
、 夹角为锐角,
夹角为锐角,所以
 =
= (t+1)>0,并且
(t+1)>0,并且 ,
,所以解得:t>-1 且t≠1.
故答案为:t>-1 且t≠1.
点评:本题主要考查向量的数量积运算,以及利用向量的数量积解决向量的夹角问题,一定注意共线的情况.

练习册系列答案
相关题目
设向量
,
是平面上的两个单位向量,它们的夹角是
,若
=
+
,
=
-2
,则向量若
与
的夹角是( )
| e1 |
| e2 |
| π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
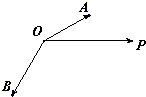 如图,已知单位向量
如图,已知单位向量