题目内容
在△ABC中,角A,B,C的对边分别为a,b,c.
(1)若a=2
,b=c=2,求角A的大小.
(2)若a=2,A=
,C=
,求b边的长.
(3)若△ABC为等腰三角形,腰AC边上的中线长为6m(m>0),求△ABC面积的最大值.(用常数m表示)
(1)若a=2
| 3 |
(2)若a=2,A=
| π |
| 3 |
| π |
| 4 |
(3)若△ABC为等腰三角形,腰AC边上的中线长为6m(m>0),求△ABC面积的最大值.(用常数m表示)
分析:(1)利用余弦定理表示出cosA,将已知的a,b及c的值代入,求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(2)由A和C的度数,利用三角形的内角和定理求出B的度数,再由a,sinA及sinB的值,利用正弦定理即可求出b的值;
(3)设BD为AC边上的中线,根据等底同高得到三角形ABD的面积与三角形BCD的面积相等,都等于三角形ABC面积的一半,然后以BD所在的直线为x轴,线段BD的垂直平分线为y轴建立平面直角坐标系,可得出B和D的坐标,设出A的坐标为(x,y),根据AB等于2AD列出关系式,整理后得到A的轨迹方程,进而确定出y的最大值即为三角形ABD中BD边上的高的最大值,由底BD为6m,利用三角形的面积公式求出三角形ABD面积的最大值,即可得到三角形ABC面积的最大值.
(2)由A和C的度数,利用三角形的内角和定理求出B的度数,再由a,sinA及sinB的值,利用正弦定理即可求出b的值;
(3)设BD为AC边上的中线,根据等底同高得到三角形ABD的面积与三角形BCD的面积相等,都等于三角形ABC面积的一半,然后以BD所在的直线为x轴,线段BD的垂直平分线为y轴建立平面直角坐标系,可得出B和D的坐标,设出A的坐标为(x,y),根据AB等于2AD列出关系式,整理后得到A的轨迹方程,进而确定出y的最大值即为三角形ABD中BD边上的高的最大值,由底BD为6m,利用三角形的面积公式求出三角形ABD面积的最大值,即可得到三角形ABC面积的最大值.
解答:解:(1)∵a=2
,b=c=2,
∴cosA=
=-
,
又A为三角形的内角,
则A=
;…(4分)
(2)∵A=
,C=
,
∴B=π-(A+C)=
,…(6分),
∴sinB=sin
=sin(
+
)=sin
cos
+cos
sin
=
,
又a=2,sinA=
,
∴由正弦定理得:
=
,
∴b=
;…(8分)
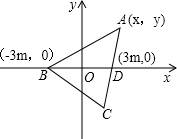
(3)设AC边上的中线为BD,则S△ABC=2S△ABD,
以BD所在直线为x轴,其垂直平分线所在直线为y轴作直角坐标系xoy,
如图所示,设点A(x,y),
则由AB=2AD得:
=2
,
整理后,得到点A的轨迹方程为(x-5m)2+y2=16m2(y≠0),
∴当x=5m时,y的最大值为4m,即△ABD中BD边上的高的最大值为4m.
∴△ABD面积的最大值为12m2,
∴△ABC面积的最大值为24m2.…(15分)
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
又A为三角形的内角,
则A=
| 2π |
| 3 |
(2)∵A=
| π |
| 3 |
| π |
| 4 |
∴B=π-(A+C)=
| 5π |
| 12 |
∴sinB=sin
| 5π |
| 12 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| ||||
| 4 |
又a=2,sinA=
| ||
| 2 |
∴由正弦定理得:
| 2 | ||||
|
| b | ||
sin
|
∴b=
3
| ||||
| 3 |

(3)设AC边上的中线为BD,则S△ABC=2S△ABD,
以BD所在直线为x轴,其垂直平分线所在直线为y轴作直角坐标系xoy,
如图所示,设点A(x,y),
则由AB=2AD得:
| (x+3m)2+y2 |
| (x-3m)2+y2 |
整理后,得到点A的轨迹方程为(x-5m)2+y2=16m2(y≠0),
∴当x=5m时,y的最大值为4m,即△ABD中BD边上的高的最大值为4m.
∴△ABD面积的最大值为12m2,
∴△ABC面积的最大值为24m2.…(15分)
点评:此题考查了正弦、余弦定理,三角形的内角和定理,特殊角的三角函数值,动点的轨迹方程,两点间的距离公式,中线的性质,其中建立适当的坐标系,得出动点A的轨迹方程,进而确定出y的最大值,即△ABD中BD边上的高的最大值是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |