题目内容
已知函数f(x)=cos(2x- )+2sin(x-
)+2sin(x- sin(x+
sin(x+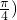 ,求函数f(x)在区间
,求函数f(x)在区间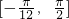 上的值域.
上的值域.
解:f(x)=cos(2x- )+2sin(x-
)+2sin(x- sin(x+
sin(x+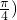
=cos(2x- )+2(sin2xcos2
)+2(sin2xcos2 -cos2xsin2
-cos2xsin2 )
)
=cos(2x- )+sin2x-cos2x=cos(2x-
)+sin2x-cos2x=cos(2x- )-cos2x
)-cos2x
=cos2xcos +sin2xsin
+sin2xsin -cos2x
-cos2x
= sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x- ),
),
∵x∈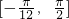 ,可得2x-
,可得2x- ∈
∈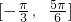
∴当2x- =
= ,即x=
,即x= 时,函数的取最大值为1
时,函数的取最大值为1
又∵f(- )=-
)=- <f(
<f( )=
)= ,
,
∴当x= 时,函数取最小值-
时,函数取最小值- ,
,
综上所述,函数f(x)=在区间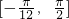 上的值域为[-
上的值域为[- ,1].
,1].
分析:将函数表达式展开,利用降次公式化简,再用辅助角公式进行合并,可得f(x)=sin(2x- ),然后利用正弦函数的图象与性质,则不难求出函数f(x)在区间
),然后利用正弦函数的图象与性质,则不难求出函数f(x)在区间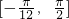 上的值域.
上的值域.
点评:本题将一个三角函数式化简,求它在闭区间上的值域,着重考查了和与差的三角函数公式、降次公式和辅助角公式,以及三角函数的值域求法等知识,属于基础题.
 )+2sin(x-
)+2sin(x- sin(x+
sin(x+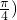
=cos(2x-
 )+2(sin2xcos2
)+2(sin2xcos2 -cos2xsin2
-cos2xsin2 )
)=cos(2x-
 )+sin2x-cos2x=cos(2x-
)+sin2x-cos2x=cos(2x- )-cos2x
)-cos2x=cos2xcos
 +sin2xsin
+sin2xsin -cos2x
-cos2x=
 sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x- ),
),∵x∈
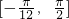 ,可得2x-
,可得2x- ∈
∈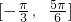
∴当2x-
 =
= ,即x=
,即x= 时,函数的取最大值为1
时,函数的取最大值为1又∵f(-
 )=-
)=- <f(
<f( )=
)= ,
,∴当x=
 时,函数取最小值-
时,函数取最小值- ,
,综上所述,函数f(x)=在区间
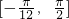 上的值域为[-
上的值域为[- ,1].
,1].分析:将函数表达式展开,利用降次公式化简,再用辅助角公式进行合并,可得f(x)=sin(2x-
 ),然后利用正弦函数的图象与性质,则不难求出函数f(x)在区间
),然后利用正弦函数的图象与性质,则不难求出函数f(x)在区间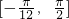 上的值域.
上的值域.点评:本题将一个三角函数式化简,求它在闭区间上的值域,着重考查了和与差的三角函数公式、降次公式和辅助角公式,以及三角函数的值域求法等知识,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )