题目内容
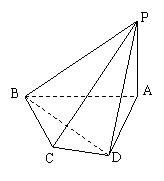
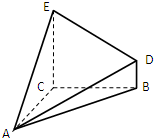 如图,四棱锥A-BCDE的底面BCDE是直角梯形,CE∥BD,∠ECB=90°,AC⊥平面BCDE,CE=CB=CA=2,BD=1.
如图,四棱锥A-BCDE的底面BCDE是直角梯形,CE∥BD,∠ECB=90°,AC⊥平面BCDE,CE=CB=CA=2,BD=1.(Ⅰ)求直线CA与平面ADE所成角的正弦值;
(Ⅱ)在线段ED上是否存在一点F,使得异面直线CF与AB所成角余弦值等
| ||
| 13 |
分析:(Ⅰ)建立空间直角坐标系,用坐标表示点与向量,求出平面ADE的法向量,即可求得直线CA与平面ADE所成角的正弦值;
(Ⅱ)假设存在λ∈(0,1),使得
=λ
,则F(0,2λ,2-λ),利用异面直线CF与AB所成角余弦值等于
,建立等式,即可求得结论.
(Ⅱ)假设存在λ∈(0,1),使得
| EF |
| ED |
| ||
| 13 |
解答: 解:(Ⅰ)如图建立空间直角坐标系,则A(2,0,0),B(0,2,0),D(0,2,1),E(0,0,2).
解:(Ⅰ)如图建立空间直角坐标系,则A(2,0,0),B(0,2,0),D(0,2,1),E(0,0,2).
∴
=(2,0,0),
=(-2,0,2),
=(0,2,-1)…(2分)
设平面ADE的法向量是
=(x,y,z),
∴
,取y=1,得
=(2,1,2),…(4分)
∴直线CA与平面ADE所成角的正弦值是|cos<
,
>|=
; …(6分)
(Ⅱ)假设存在λ∈(0,1),使得
=λ
,则F(0,2λ,2-λ),
∴
=(0,2λ,2-λ),
∵
=(-2,2,0),∴|cos<
,
>|=
…(8分)
令
=
,解得λ=-1,或λ=
,…(10分)
∵λ∈(0,1),∴λ=
,…(11分)
∴当F是线段线段ED的中点时,异面直线CF与AB所成角余弦值等于
.…(12分)
 解:(Ⅰ)如图建立空间直角坐标系,则A(2,0,0),B(0,2,0),D(0,2,1),E(0,0,2).
解:(Ⅰ)如图建立空间直角坐标系,则A(2,0,0),B(0,2,0),D(0,2,1),E(0,0,2).∴
| CA |
| AE |
| ED |
设平面ADE的法向量是
| m |
∴
|
| m |
∴直线CA与平面ADE所成角的正弦值是|cos<
| CA |
| m |
| 2 |
| 3 |
(Ⅱ)假设存在λ∈(0,1),使得
| EF |
| ED |
∴
| CF |
∵
| AB |
| CF |
| AB |
| ||
|
令
| ||
|
| ||
| 13 |
| 1 |
| 2 |
∵λ∈(0,1),∴λ=
| 1 |
| 2 |
∴当F是线段线段ED的中点时,异面直线CF与AB所成角余弦值等于
| ||
| 13 |
点评:本题考查利用空间向量解决立体几何问题,解题的关键是建立坐标系,用向量表示点与坐标.

练习册系列答案
相关题目
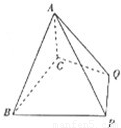
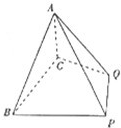 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
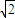 BC,AB=AC=
BC,AB=AC=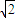 B.
B.
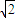 BC,AB=AC=
BC,AB=AC=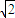 B.
B.