题目内容

设[x]表示不超过x的最大整数，又设x，y满足方程组，如果x不是整数，那么x＋y的取值范围是(　　)

A．(35,39)                         B．(49,51)

C．(71,75)                         D．(93,94)

解析：∵[x－3]＝[x]－3，

解，

得[x]＝20，y＝73，

∵x不是整数，

∴20＜x＜21，

∴93＜x＋y＜94.

答案：D

练习册系列答案
相关题目
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数
C
x
8
的值域是（　　）
A、[
16
3
，28]
B、[
16
3
，56)
C、(4，
28
3
)∪[28，56）
D、(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数（如：[1]=1，[
5
2
]=2），则定义在[2，4）的函数f（x）=x[x]-ax（其中a为常数，且a≤4）的值域为（　　）
A、[4-2a，64-4a）
B、[4-2a，9-3a）∪[27-3a，64-4a）
C、[9-3a，64-4a）
D、[4-2a，9-3a]∪（27-3a，64-4a]
（2010•台州二模）设[x]表示不超过x的最大整数（如[2]=2，[1.3]=1），已知函数f(x)=
[x+
1
2
]
[x]+
1
2
（x≥0），当f（x）＜1时，实数x的取值范围是
{x|k≤x＜k+
1
2
，k∈N}
{x|k≤x＜k+
1
2
，k∈N}
．
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
Cxn
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数C8x的值域是（　　）
A．[
16
3
，28]		B．[
16
3
，56)
C．(4，
28
3
)∪[28，56）		D．(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数，（如[2]=2，=1），对于给定的n∈N+，定义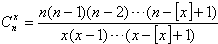，x∈[1，+∞），则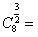（    ），当x∈[2，3）时，函数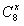的值域是（    ）。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网