题目内容
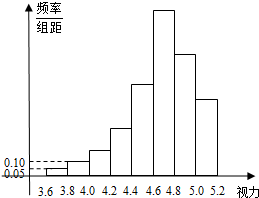 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力,按视力情况分成8组,得到如图所示的频率分布直方图,但不慎将部分数据丢失,只知道前6组的频数从左到右依次是等比数列{an}的前六项,后3组的频数从左到右依次是等差数列{bn}的前三项.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力,按视力情况分成8组,得到如图所示的频率分布直方图,但不慎将部分数据丢失,只知道前6组的频数从左到右依次是等比数列{an}的前六项,后3组的频数从左到右依次是等差数列{bn}的前三项.(1)求数列{an}和{bn}的通项公式;
(2)设数列{cn}满足cn=
| 35-bn | 3an |
分析:(1)依题意可求得a1,a2,从而可求得等比数列{an}的公比,继而可求得其通项公式,同理可求得b1及其公差d,继而可求得其通项公式;
(2)由于cn=(3n-2)•(
)n-1,可列出Sn的表示式,利用错位相减法求和即可.
(2)由于cn=(3n-2)•(
| 1 |
| 2 |
解答:解:(1)由题意知:a1=0.05×0.2×100=1,
a2=0.1×0.2×100=2.
因此,数列{an}是一个首项为1,公比为2的等比数列,所以an=2n-1.
b1=a6=32,b1+b2+b3=100-(a1+a2+…+a5)=69,
所以3b1+
d=69,解得d=-9,
因此,数列{bn}是一个首项为32,公差为-9的等差数列,
所以bn=-9n+41.
(2)cn=
=
=(3n-2)•(
)n-1,则
Sn=1×(
)0+4×(
)1+7×(
)2+…+(3n-2)×(
)n-1 ①
Sn=1×(
)1+4×(
)2+7×(
)3+…+(3n-5)×(
)n-1+(3n-2)×(
)n②
故①-②得:
Sn=1+3×(
)1+3×(
)2+3×(
)3+…+3×(
)n-1-(3n-2)×(
)n
∴
Sn=1+3×
-(3n-2)×(
)n=4-
,
∴Sn=8-
.
a2=0.1×0.2×100=2.
因此,数列{an}是一个首项为1,公比为2的等比数列,所以an=2n-1.
b1=a6=32,b1+b2+b3=100-(a1+a2+…+a5)=69,
所以3b1+
| 3×2 |
| 2 |
因此,数列{bn}是一个首项为32,公差为-9的等差数列,
所以bn=-9n+41.
(2)cn=
| 35-(-9n+41) |
| 3×2n-1 |
| 3n-2 |
| 2n-1 |
| 1 |
| 2 |
Sn=1×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
| 3n+4 |
| 2n |
∴Sn=8-
| 3n+4 |
| 2n-1 |
点评:本题考查数列求和,着重考查等差数列与等比数列的通项公式,错位相减法求和,考查观察、分析与运算能力,属于难题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
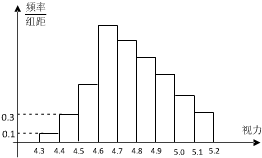 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为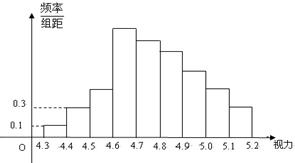 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项. 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为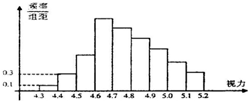 (2009•淄博一模)为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数b,则a、b的值分别为( )
(2009•淄博一模)为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数b,则a、b的值分别为( ) (2012•黄州区模拟)为了解某校高三学生的视力情况,随机地抽查了该校100名学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,只知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.1之间的学生人数为b,则a和b的值分别为( )
(2012•黄州区模拟)为了解某校高三学生的视力情况,随机地抽查了该校100名学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,只知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.1之间的学生人数为b,则a和b的值分别为( )