题目内容
过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若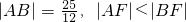 ,则|AF|=________.
,则|AF|=________.

分析:设出点的坐标与直线的方程,利用抛物线的定义表示出|AF|、|BF|再联立直线与抛物线的方程利用根与系数的关系解决问题,即可得到答案.
解答:由题意可得:F(
 ,0),设A(x1,y1),B(x2,y2).
,0),设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,
所以|AF|=
 +x1,|BF|=
+x1,|BF|= +x2.
+x2.因为
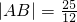 ,所以x1+x2=
,所以x1+x2=
设直线l的方程为y=k(x-
 ),
),联立直线与抛物线的方程可得:k2x2-(k2+2)x+
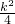 =0,
=0,所以x1+x2=
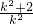 .
.∴
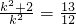
∴k2=24
∴24x2-26x+6=0,
∴
 ,
,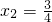
∴|AF|=
 +x1=
+x1=
故答案为:

点评:解决此类问题的关键是熟练掌握抛物线的定义,以及掌握直线与抛物线位置关系,并且结合准确的运算也是解决此类问题的一个重要方面

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,若
-
=1,则直线l的倾斜角θ(0<θ≤
)等于( )
| 1 |
| |AF| |
| 1 |
| |BF| |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过抛物线y2=2x的焦点作一条直线与抛物线交于两点,它们的横坐标之和等于2,则这样的直线( )
| A、有且只有一条 | B、有且只有两条 | C、有且只有三条 | D、有且只有四条 |