题目内容
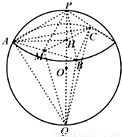
同底的两个正三棱锥内接于半径为R的球,它们的侧面与底面所成角分别为α1、α2,求:(1)侧面积的比;
(2)体积的比;
(3)角α1+α2的最大值.
解析:如图,(1)设O为球心,O1为正三棱锥底面ABC所在圆的圆心,两个三棱锥的顶点分别为P、Q,取BC的中点D,则PD⊥BC,AD⊥BC,

∴∠PDO1是侧面与底面所成二面角的平面角.
∴∠PDO1=α1.同理,∠QDO1=α2.
∴PD=![]() .
.
∴SP—ABC侧=3·![]() BC·PD=
BC·PD=![]() BC·
BC·![]() .∴SQ—ABC侧=3·
.∴SQ—ABC侧=3·![]() BC·QD=
BC·QD=![]() ·BC·
·BC·![]() .
.
∴SP—ABC侧∶SQ—ABC侧=cosα2∶cosα1.
(2)PO1=DO1·tanα1,QO1=DO1·tanα2,
这两个三棱锥的底都是△ABC,∴VP—ABC∶VQ—ABC=PQ1∶QO1=tanα1∶tanα2.
(3)设三角形ABC边长为a,OO1=h,
则tanα1=![]() ,tanα2=
,tanα2=![]() .而DO1=
.而DO1=![]() ,
,
AO1=![]() a,R2-h2=AO12=
a,R2-h2=AO12=![]() a2,
a2,
∴tan(α1+α2)=
∴![]() <α1+α2<π.
<α1+α2<π.
当平面ABC通过球心O,a最大为![]() R时,
R时,
tan(α1+α2)取最大值-![]() ,这时α1+α2也最大,最大值为π-arctan
,这时α1+α2也最大,最大值为π-arctan![]() .
.

练习册系列答案
相关题目
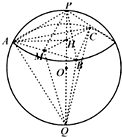 如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是
如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是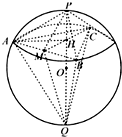 如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是________.
如图,设同底的两个正三棱锥P-ABC和Q-ABC 内接于同一个球O.若正三棱锥P-ABC的侧面与底面所成的角为 45°,则正三棱锥Q-ABC的侧面与底面所成角的正切值是________.