题目内容
设函数y=f(x)是定义在R上的函数,当x<0时,f(x)>1,对任意实数x、y∈R,有?f(x+y)=f(x)·f(y).?(1)求证:f(0)=1,且当x>0时,有0<f(x)<1.
(2)若数列{an}满足a1=f(0),且f(an+1)=![]() ,n∈N*.
,n∈N*.
①求an;
②若不等式(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )≥k·
)≥k·![]() ,对于n∈N*都成立,求k的最大值.
,对于n∈N*都成立,求k的最大值.
(1)证明:∵x、y∈R,有f(x+y)=f(x)·f(y),
∴取y=0,x<0,则f(x)=f(x)f(0)![]() x<0时f(x)>1,∴f(0)=1.
x<0时f(x)>1,∴f(0)=1.
又设x>0,y=-x<0,则1=f(0)=f(x)f(-x),
∴f(x)=![]() .
.
而当-x<0时,f(-x)>1,∴当x>0时,0<f(x)<1.
(2)解:①{an}中,a1=f(0)=1,由f(an+1)=![]() ,得f(an+1)f(-an-2)=1=f(0),
,得f(an+1)f(-an-2)=1=f(0),
∴f(an+1-an-2)=f(0).
可证y=f(x)是R上的递减函数,证明如下:
设x1、x2∈R且x1<x2,则x2=x1+t(t>0),f(t)∈(0,1).
∴f(x2)=f(x1+t)=f(x1)f(t)<f(x1),即?f(x2)<f(x1).∴f(x)是R上的减函数.
∴?an+1-an-2=0,即an+1-an=2.∴an=2n-1.
②设g(n)= ,得
,得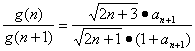 .
.
∴![]() <1.
<1.
∴![]() <1,即g(n)<g(n+1).
<1,即g(n)<g(n+1).
∴g(n)对n∈N*单调递增.而k≤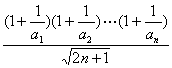 恒成立,
恒成立,
即k≤g(n)对n∈N*恒成立.∴k≤g(1)=![]() ,即k≤
,即k≤![]() .∴k的最大值为
.∴k的最大值为![]() .
.

练习册系列答案
相关题目