题目内容
设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,…
若b1>c1,b1+c1=2a1,an+1=an,bn+1=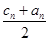 ,cn+1=
,cn+1= ,则( )
,则( )
| A.{Sn}为递减数列 |
| B.{Sn}为递增数列 |
| C.{S2n-1}为递增数列,{S2n}为递减数列 |
| D.{S2n-1}为递减数列,{S2n}为递增数列 |
B;
解析

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
数列1,-3,5,-7,9,……的一个通项公式为
A. | B. |
C. | D. |
用火柴棒摆“金鱼”,如图所示: 
按照上面的规律,第 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )
A. | B. | C. | D. |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第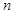 行有
行有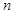 个数且两端的数均为
个数且两端的数均为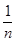
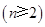 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如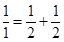 ,
,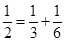 ,
,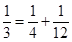 ,…,则第10行第4个数(从左往右数)为( )
,…,则第10行第4个数(从左往右数)为( )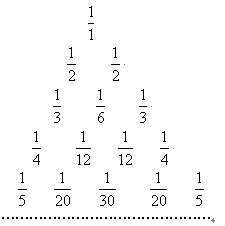
A.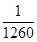 | B.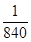 | C.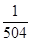 | D. |
数列 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于( ).
等于( ).
A. | B. | C. | D. |
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求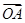 ·
·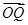 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin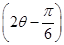 的值.
的值.
已知数列{an}满足a1=1,an+1= ,则其前6项之和是( )
,则其前6项之和是( )
| A.16 | B.20 | C.33 | D.120 |
设数列 的前n项和为
的前n项和为 ,令
,令 ,称
,称 为数列
为数列 ,
, ,……,
,……, 的“平均和”,已知数列
的“平均和”,已知数列 ,
, ,……,
,……, 的“平均和”为2004,那么数列2,
的“平均和”为2004,那么数列2,  ,
, ,……,
,……, 的“平均和”为( )
的“平均和”为( )
| A.2002 | B.2004 | C.2006 | D.2008 |