题目内容
已知函数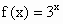 ,且
,且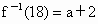 ,
,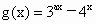 的定义域为[0,1].
的定义域为[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性,并试用定义证明;
(3)求g(x)的值域.
答案:略
解析:
解析:
|
解: (1)∵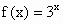 ,且 ,且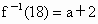 , ,
∴ 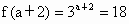 . .
∴ 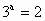 . .
∵  , ,
∴  . .
(2)∵函数g(x)的定义域[0,1], 令 ∴tÎ
[1,2],则 ∵函数
∴g(x)在[0,1]上单调递减. 证明:设 ∴ = 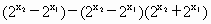
= 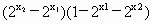 . .
∵ 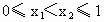 , ,
∴  且 且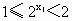 , ,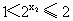 , ,
∴ 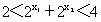 . .
∴ 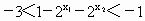 . .
∴可知 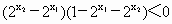 , ,
∴ 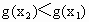 . .
∴函数 g(x)在[0,1]上单调递减.(3)∵g(x)在[0,1]上减函数,则xÎ [0,1],有g(1)≤g(x)≤g(0). ∵
故函数g(x)的值域为[-2,0]. |

练习册系列答案
相关题目
 ,∴xÎ
[0,1]时,函数t在区间[0,1]单调递增,
,∴xÎ
[0,1]时,函数t在区间[0,1]单调递增, ,tÎ
[1,2].
,tÎ
[1,2]. 在[0,1]上单调递增,
在[0,1]上单调递增, 在[1,2]上单调递减,
在[1,2]上单调递减, ,
, 为区间[0,1]内任意两值,且
为区间[0,1]内任意两值,且 ,
,
 ,
, ,∴-2≤g(x)≤0.
,∴-2≤g(x)≤0. ,且
,且 ,
, 的定义域为[0,1].
的定义域为[0,1].