题目内容
(本小题满分12分)
已知圆C: ,直线
,直线 过定点A (1,0).
过定点A (1,0).
(1)若 与圆C相切,求
与圆C相切,求 的方程;
的方程;
(2)若 与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线
与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线 的方程.
的方程.
【答案】
(1)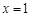 或
或 (2)
(2) 或
或
【解析】
试题分析:(1) ①若直线 的斜率不存在,则直线
的斜率不存在,则直线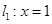 ,符合题意. ……2分
,符合题意. ……2分
②若直线 斜率存在,设直线
斜率存在,设直线 的方程为
的方程为 ,即
,即 .
.
由题意知,圆心(3,4)到已知直线 的距离等于半径2,
的距离等于半径2,
即:  ,解之得
,解之得  .
.
所以所求直线 的方程是
的方程是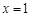 或
或 . ……6分
. ……6分
(2)因为直线与圆相交,所以斜率必定存在,且不为0,
设直线方程为 ,
,
则圆心到直线 的距离为
的距离为 ,
,
又∵△CPQ的面积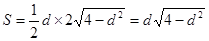 =
=
∴ 当d=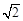 时,S取得最大值2.
时,S取得最大值2.
∴ =
=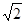 ,∴
,∴ 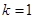 或
或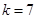 ,
,
所以所求直线 方程为
方程为 或
或 . ……12分
. ……12分
考点:本小题主要考查直线圆的位置关系的求解和应用、直线方程的求解和三角函数面积公式的应用以及二次函数求最值,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:设直线方程的点斜式时,要考虑直线的斜率存在与不存在两种情况,不能漏掉直线斜率不存在的情形.

练习册系列答案
相关题目