题目内容
若函数f(x)满足下列两个性质:
①f(x)在其定义域上是单调增函数或单调减函数;
②在f(x)的定义域内存在某个区间使得f(x)在[a,b]上的值域是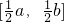 .则我们称f(x)为“内含函数”.
.则我们称f(x)为“内含函数”.
(1)判断函数 是否为“内含函数”?若是,求出a、b,若不是,说明理由;
是否为“内含函数”?若是,求出a、b,若不是,说明理由;
(2)若函数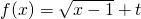 是“内含函数”,求实数t的取值范围.
是“内含函数”,求实数t的取值范围.
解:(1)∵函数 ,其定义域为[0,+∞),∴函数
,其定义域为[0,+∞),∴函数 在区间[0,+∞)上是单调增函数.
在区间[0,+∞)上是单调增函数.
设 在区间[a,b]上的值域是
在区间[a,b]上的值域是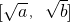 .
.
由 ,解得
,解得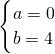 .
.
故函数 是“内含函数”,且a=0,b=4.
是“内含函数”,且a=0,b=4.
(2)设g(x)=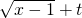 ,其定义域为[1,+∞),且在定义域上单调递增.
,其定义域为[1,+∞),且在定义域上单调递增.
∵g(x)为“内含函数”,∴存在区间[a,b]?[1,+∞),满足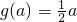 ,
,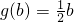 .
.
即方程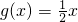 在区间[1,+∞)内有两个不等实根.
在区间[1,+∞)内有两个不等实根.
也即方程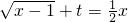 在区间[1,+∞)内有两个不等实根,令
在区间[1,+∞)内有两个不等实根,令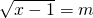 ,则其可化为:
,则其可化为:
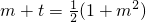 ,即方程m2-2m+(1-2t)=0有两个非负的不等实根x1、x2.
,即方程m2-2m+(1-2t)=0有两个非负的不等实根x1、x2.
∴ 解得
解得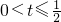 .
.
∴实数t的取值范围是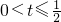 .
.
分析:(1)根据新定义“内含函数”,要满足两条:一是在其定义域上是单调函数,二是在定义域内存在某个区间[a,b],且在此区间上的值域是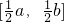 即可.
即可.
(2)若函数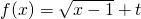 是“内含函数”,其定义域为[1,+∞),且在定义域上单调递增,满足第一条;只要t再满足:存在区间[a,b]?[1,+∞),满足
是“内含函数”,其定义域为[1,+∞),且在定义域上单调递增,满足第一条;只要t再满足:存在区间[a,b]?[1,+∞),满足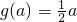 ,
,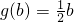 ,即可.
,即可.
点评:充分理解新定义是进行判断的前提.其关键是看在定义域内方程f(x)= x是否存在两个不等的实数根.
x是否存在两个不等的实数根.
 ,其定义域为[0,+∞),∴函数
,其定义域为[0,+∞),∴函数 在区间[0,+∞)上是单调增函数.
在区间[0,+∞)上是单调增函数.设
 在区间[a,b]上的值域是
在区间[a,b]上的值域是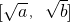 .
.由
 ,解得
,解得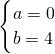 .
.故函数
 是“内含函数”,且a=0,b=4.
是“内含函数”,且a=0,b=4.(2)设g(x)=
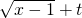 ,其定义域为[1,+∞),且在定义域上单调递增.
,其定义域为[1,+∞),且在定义域上单调递增.∵g(x)为“内含函数”,∴存在区间[a,b]?[1,+∞),满足
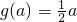 ,
,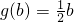 .
.即方程
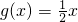 在区间[1,+∞)内有两个不等实根.
在区间[1,+∞)内有两个不等实根.也即方程
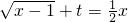 在区间[1,+∞)内有两个不等实根,令
在区间[1,+∞)内有两个不等实根,令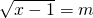 ,则其可化为:
,则其可化为: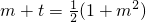 ,即方程m2-2m+(1-2t)=0有两个非负的不等实根x1、x2.
,即方程m2-2m+(1-2t)=0有两个非负的不等实根x1、x2.∴
 解得
解得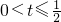 .
.∴实数t的取值范围是
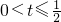 .
.分析:(1)根据新定义“内含函数”,要满足两条:一是在其定义域上是单调函数,二是在定义域内存在某个区间[a,b],且在此区间上的值域是
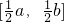 即可.
即可.(2)若函数
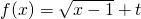 是“内含函数”,其定义域为[1,+∞),且在定义域上单调递增,满足第一条;只要t再满足:存在区间[a,b]?[1,+∞),满足
是“内含函数”,其定义域为[1,+∞),且在定义域上单调递增,满足第一条;只要t再满足:存在区间[a,b]?[1,+∞),满足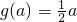 ,
,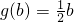 ,即可.
,即可.点评:充分理解新定义是进行判断的前提.其关键是看在定义域内方程f(x)=
 x是否存在两个不等的实数根.
x是否存在两个不等的实数根. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)为R上的连续函数且存在反函数f-1(x),若函数f(x)满足下表:

那么,不等式|f-1(x-1)|<2的解集是( )

那么,不等式|f-1(x-1)|<2的解集是( )
A、{x|
| ||
B、{x|
| ||
| C、{x|1<x<2} | ||
| D、{x|1<x<5} |

 <x<4}
<x<4} <x<3}
<x<3}
 <x<4}
<x<4} <x<3}
<x<3}