Question

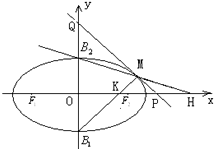（2011•通州区一模）已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率e=

4

5

，两焦点为F₁，F₂，B₁，B₂为椭圆C短轴的两端点，动点M在椭圆C上．且△MF₁F₂的周长为18．
（I）求椭圆C的方程；
（II）当M与B₁，B₂不重合时，直线B₁M，B₂M分别交x轴于点K，H．求

OH

•

OK

的值；
（III）过点M的切线分别交x轴、y轴于点P、Q．当点M在椭圆C上运动时，求|PQ|的最小值；并求此时点M的坐标．

Answer 1

分析：（I）由e=

4

5

，得

c

a

=

4

5

①，由△MF₁F₂的周长为18，得a+c=9②．联立①②解得a，c，根据b²=a²-c²可求得b；
（II）由（I）易求B₁，B₂坐标，设M（x₀，y₀）（x₀≠0），由点斜式可得直线B₁M的方程、直线B₂M的方程，由直线方程可得点K、H坐标，通过计算可得

OH

•

OK

的值；
（III）设切线方程为：y=kx+m（k≠0），代入椭圆方程得，（25k²+9）x²+50kmx+25m²-225=0（*），则△=0，点P（-

m

k

，0），Q（0，m），由两点间距离公式可得|PQ|²，利用基本不等式求其最小值，由等号成立条件可求得k值，进而得m值，再代入（*）式可得点M横坐标，进而得纵坐标，根据对称性可得其它象限的坐标；

解答：解：（I）由e=

4

5

，得

c

a

=

4

5

①，
由△MF₁F₂的周长为18，得2a+2c=18，即a+c=9②．
联立①②解得a=5，c=4，所以b²=a²-c²=9，
所以椭圆C的方程为：

x2

25

+

y2

9

=1；
（II）由（I）可得B₁（0，-3），B₂（0，3），
设M（x₀，y₀）（x₀≠0），则直线B₁M的方程为：y=

y0+3

x0

x-3，直线B₂M的方程为：y=

y0-3

x0

x+3，
令y=0，得xK=

3x0

y0+3

，xH=

-3x0

y0-3

，则

OH

=(

-3x0

y0-3

，0)，

OK

=(

3x0

y0+3

，0)，
所以

OH

•

OK

=

-3x0

y0-3

×

3x0

y0+3

=

-9x02

y02-9

，
又

x02

25

+

y02

9

=1，所以y02-9=-

9

25

x02，代入上式，得

OH

•

OK

=

-9x02

- 9 25 x02

=25；
（III）设切线方程为：y=kx+m（k≠0），代入椭圆方程得，（25k²+9）x²+50kmx+25m²-225=0（*），
则△=（50km）²-4（25k²+9）（25m²-225）=0，即m²=25k²+9①，
点P（-

m

k

，0），Q（0，m），
则|PQ|²=

m2

k2

+m2=m2(1+

1

k2

)=(25k2+9)(1+

1

k2

)=25k2+

9

k2

+34≥2

25k2• 9 k2

+34=64，
当且仅当k2=

3

5

，即k=±

15

5

时取等号，
所以|PQ|的最小值为8，
此时m²=25k²+9=24，所以m=±2

6

，
当m=2

6

，k=

15

5

时，代入（*）式并化简得8x2+20

10

x+125=0，
解得x=-

5 10

4

，y=

15

5

×（-

5 10

4

）+2

6

=

3 6

4

，
此时点M（-

5 10

4

，

3 6

4

），
由椭圆的对称性可得当点M在第一、三、四象限时坐标分别为：（

5 10

4

，

3 6

4

），（-

5 10

4

，-

3 6

4

），（

5 10

4

，-

3 6

4

）．

点评：本题考查椭圆方程、直线与椭圆的位置关系，考查向量的数量积运算、基本不等式求最值，考查学生分析解决问题的能力．