题目内容

任意的|m|≤2，函数f（x）=mx²-2x+1-m恒为负，则x的取值范围为________．

$\text{[math]}$
分析：变换主元，把m作为主元，x看成系数，即可求解．
解答：∵任意的|m|≤2，函数f（x）=mx²-2x+1-m恒为负，
∴任意的|m|≤2，（x²-1）m-2x+1＜0恒成立，
设g（m）=（x²-1）m-2x+1，则任意的|m|≤2，g（m）＜0恒成立
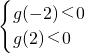
∴ $\text{[math]}$
∴ $\text{[math]}$
∴ $\text{[math]}$ ＜x＜ $\text{[math]}$
故答案为 $\text{[math]}$ ．
点评：本题考查恒成立问题，考查解不等式，考查学生分析转化问题的能力，属于中档题．

练习册系列答案

金考卷周末培优系列答案

名校名师课时作业系列答案

新思维闯关100分系列答案

同步精练与单元检测系列答案

每课必练系列答案

人教金学典同步解析与测评系列答案

金牌作业本系列答案

孟建平系列丛书浙江考题系列答案

导学与演练系列答案

巧学巧练系列答案

相关题目

已知函数f（x）对任意的x，y∈R，总有f（x）+f（y）=f（x+y），且x＜0时，f（x）＞0．
（1）求证：函f（x）是奇函数；
（2）求证：函数f（x）是R上的减函数；
（3）若定义在（-2，2）上的函数f（x）满足f（-m）+f（1-m）＜0，求实数m的取值范围．

（2011•遂宁二模）设函数f（x）的定义域为D，若存在非零实数，使得对于任意x∈M（M⊆D），有x+l∈D，f（x+l）≥f（x），则称f（x）为M上的l高调函数，现给出下列命题：
①函数f(x)=(

)x为R上的1高调函数；
②函数f （x）=sin 2x为R上的高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x²为[-1，+∞）上的m高调函数，那么实数m的取值范围是[2，+∞）；
④如果定义域为R的函教f （x）是奇函数，当x≥0时，f（x）=|x-a²|-a²，且f（x）为R上的4高调函数，那么实数a的取值范围是[一1，1]．
其中正确的命题是

（写出所有正确命题的序号）．

已知集合M是满足下列条件的函数f（x）的全体：（1）当x∈[0，+∞）时，函数值为非负实数；（2）对于任意的s、t，都有f（s）+f（t）≤f（s+t）；在三个函数f₁（x）=x，f₂（x）=2^x-1，f₃（x）=ln（x+1）中，属于集合M的是

已知集合M是满足下列条件的函数f（x）的全体：（1）当x∈[0，+∞）时，函数值为非负实数；（2）对于任意的s、t，都有f（s）+f（t）≤f（s+t）；在三个函数f₁（x）=x，f₂（x）=2^x-1，f₃（x）=ln（x+1）中，属于集合M的是______．

设函数f（x）的定义域为D，若存在非零实数，使得对于任意x∈M（M⊆D），有x+l∈D，f（x+l）≥f（x），则称f（x）为M上的l高调函数，现给出下列命题：
①函数

为R上的1高调函数；
②函数f （x）=sin 2x为R上的高调函数；
③如果定义域是[-1，+∞）的函数f（x）=x²为[-1，+∞）上的m高调函数，那么实数m的取值范围是[2，+∞）；
④如果定义域为R的函教f （x）是奇函数，当x≥0时，f（x）=|x-a²|-a²，且f（x）为R上的4高调函数，那么实数a的取值范围是[一1，1]．
其中正确的命题是（写出所有正确命题的序号）．