题目内容
(不等式选讲选做题)对于任意实数a(a≠0)和b,不等式 恒成立,试求实数x的取值范围是________.
恒成立,试求实数x的取值范围是________.
[0,2]
分析:由题意可得 小于或等于
小于或等于 的最小值,故所求x的范围即为不等式
的最小值,故所求x的范围即为不等式
≤2的解集.再根据数轴上0和2对应点到 和
和 对应点的距离之和等于2,可得实数x的取值范围.
对应点的距离之和等于2,可得实数x的取值范围.
解答:由题意可得 ≤
≤ 恒成立,
恒成立,
故 小于或等于
小于或等于 的最小值,
的最小值,
而 的最小值等于2,故所求x的范围即为不等式
的最小值等于2,故所求x的范围即为不等式 ≤2的解集.
≤2的解集.
由于 表示数轴上的x对应点到
表示数轴上的x对应点到 和
和 对应点的距离之和,
对应点的距离之和,
又由于数轴上0和2对应点到 和
和 对应点的距离之和等于2,
对应点的距离之和等于2,
故不等式 ≤2的解集为[0,2],
≤2的解集为[0,2],
故答案为[0,2].
点评:本题考查绝对值的意义,绝对值不等式的解法,判断于 表示数轴上的x对应点到
表示数轴上的x对应点到 和
和 对应点的
对应点的
距离之和,是解题的关键,属于中档题.
分析:由题意可得
 小于或等于
小于或等于 的最小值,故所求x的范围即为不等式
的最小值,故所求x的范围即为不等式
≤2的解集.再根据数轴上0和2对应点到
 和
和 对应点的距离之和等于2,可得实数x的取值范围.
对应点的距离之和等于2,可得实数x的取值范围.解答:由题意可得
 ≤
≤ 恒成立,
恒成立,故
 小于或等于
小于或等于 的最小值,
的最小值,而
 的最小值等于2,故所求x的范围即为不等式
的最小值等于2,故所求x的范围即为不等式 ≤2的解集.
≤2的解集.由于
 表示数轴上的x对应点到
表示数轴上的x对应点到 和
和 对应点的距离之和,
对应点的距离之和,又由于数轴上0和2对应点到
 和
和 对应点的距离之和等于2,
对应点的距离之和等于2,故不等式
 ≤2的解集为[0,2],
≤2的解集为[0,2],故答案为[0,2].
点评:本题考查绝对值的意义,绝对值不等式的解法,判断于
 表示数轴上的x对应点到
表示数轴上的x对应点到 和
和 对应点的
对应点的距离之和,是解题的关键,属于中档题.

练习册系列答案
相关题目
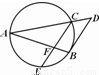
 ,则线段CD的长为 .
,则线段CD的长为 .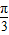 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .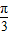 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .