题目内容
设椭圆
=1(a＞b＞0)的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆和x轴正半轴于P、Q两点，且P分向量
所成的比为8：5．(Ⅰ)求椭圆的离心率；
(Ⅱ)若过A、Q、F三点的圆恰好与直线l：x+
y+3=0相切，求椭圆方程．
解：(Ⅰ)设点Q(x0，0)，F(-c，0)，
其中c=，A(0，b)．
由P分所成的比为8：5，得P(x0, 
b)，
∴(
)2
a． ①
而
=(c，b)，
=(x0，-b)，
⊥
，
∴
·
=0，∴cx0-b2=0，x0=
． ②
由①②知2b2=3ac，∴2c2+3ac-2a2=0．
∴2e2+3e-2=0，∴e=
．
(Ⅱ)满足条件的圆心为O′(
，0)，
=c，∴O′(c，0)
圆半径r=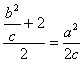
=a.
由圆与直线l：
x+
y+3=0相切得，
=a,
又a=2c，∴c=1，a=2，b=
．
∴椭圆方程为
=1．
练习册系列答案
相关题目
=1(a＞b＞0)的右焦点为F1，右准线为l1,若过点F1且垂直于x轴的弦长等于点F1到准线l1的距离，则椭圆的离心率是_________.
=1(a＞b＞0)的面积为πab,过坐标原点的直线l、x轴的正半轴及椭圆围成的两个区域的面积分别为s、t(如图),则s关于t的函数图象的大致形状为
+
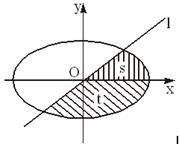
=1(a＞b＞0)的左焦点为F1(－2,0),左准线l1与x轴交于点N(－3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.