题目内容
数列{an}中,a1=1,且an+1=2an+1,又设bn=an+1(1)求证:数列{bn}是等比数列;
(2)求数列{an}的通项公式;
(3)设
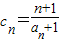 (n∈N*),求数列{cn}的前n项的和Sn.
(n∈N*),求数列{cn}的前n项的和Sn.
【答案】分析:(1)直接对条件an+1=2an+1整理即可得到an+1+1=2(an+1)进而得到数列{bn}是等比数列;
(2)根据第一问的结论先求出数列{bn}通项公式;再结合bn=an+1即可求数列{an}的通项公式;
(3)先求出数列{cn}的通项公式,再利用乘公比错位相减法求和即可.
解答:解:(1)∵a1=1,且an+1=2an+1,bn=an+1
∴an+1+1=2(an+1)
∴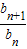 =2,a1+1=2
=2,a1+1=2
∴数列{bn}是首项为2,公比为2的等比数列.
(2)∵bn=2×2n-1=2n
∴an=bn-1=2n-1
(3)∵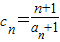 =
=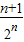 .
.
∴Sn=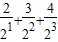 +…+
+…+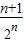
∴ Sn=
Sn=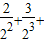 …+
…+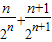
∴两式相减可得: Sn=
Sn=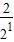 +
+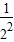 +
+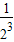 +…+
+…+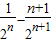 =1+
=1+ -
-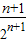 =
=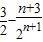 .
.
∴Sn=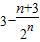 .
.
点评:本题主要考查了利用数列的递推公式求解数列的通项公式.解决第三问用到了乘公比错位相减求数列的和,乘公比错位相减求数列的和是数列部分的重要方法,要注意掌握,它适用于一等差数列乘以一等比数列组合而成的新数列的求和.
(2)根据第一问的结论先求出数列{bn}通项公式;再结合bn=an+1即可求数列{an}的通项公式;
(3)先求出数列{cn}的通项公式,再利用乘公比错位相减法求和即可.
解答:解:(1)∵a1=1,且an+1=2an+1,bn=an+1
∴an+1+1=2(an+1)
∴
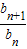 =2,a1+1=2
=2,a1+1=2∴数列{bn}是首项为2,公比为2的等比数列.
(2)∵bn=2×2n-1=2n
∴an=bn-1=2n-1
(3)∵
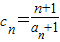 =
=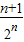 .
.∴Sn=
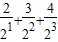 +…+
+…+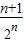
∴
 Sn=
Sn=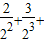 …+
…+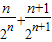
∴两式相减可得:
 Sn=
Sn=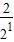 +
+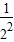 +
+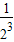 +…+
+…+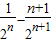 =1+
=1+ -
-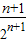 =
=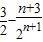 .
.∴Sn=
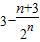 .
.点评:本题主要考查了利用数列的递推公式求解数列的通项公式.解决第三问用到了乘公比错位相减求数列的和,乘公比错位相减求数列的和是数列部分的重要方法,要注意掌握,它适用于一等差数列乘以一等比数列组合而成的新数列的求和.

练习册系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|