题目内容
三次函数f(x)=x3-2bx+2b在[1,2]内恒为正值的充要条件为( )
分析:原问题等价于函数y1=x3,y2=2b(x-1),当x∈[1,2]时,恒有y2<y1成立,由直线和曲线的相切可得b的取值范围.
解答:解:原问题等价于函数y1=x3,y2=2b(x-1),
当x∈[1,2]时,恒有y2<y1成立,
由于[1,2],讨论第一象限即可,
直线y2过(1,0)点,斜率为2b.
在[1,2]范围内,直线y2与y1=x3相切时的斜率即是2b的最大值.
对y1求导得相切的斜率3x2,由2b=3x2可得b的最大值为
x2.
联立方程组
,解之可得x=
,y=
,
即切点为(
,
),可知只需b<
x2=
即可
故可得其充要条件为:b<
故选B
当x∈[1,2]时,恒有y2<y1成立,
由于[1,2],讨论第一象限即可,
直线y2过(1,0)点,斜率为2b.
在[1,2]范围内,直线y2与y1=x3相切时的斜率即是2b的最大值.
对y1求导得相切的斜率3x2,由2b=3x2可得b的最大值为
| 3 |
| 2 |
联立方程组
|
| 3 |
| 2 |
| 27 |
| 8 |
即切点为(
| 3 |
| 2 |
| 27 |
| 8 |
| 3 |
| 2 |
| 27 |
| 8 |
故可得其充要条件为:b<
| 27 |
| 8 |
故选B
点评:本题考查充要条件的求解,把问题转化为求函数的导数和图象的公共点问题是解决问题的关键,属中档题.

练习册系列答案
相关题目
 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-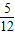 的对称中心为 ;
的对称中心为 ; +…+f(
+…+f(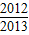 )= .
)= .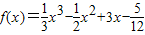 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-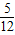 的对称中心为 ;
的对称中心为 ;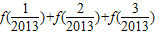 +…+f(
+…+f(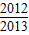 )= .
)= .