题目内容
平面内给定三个向量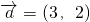 ,
,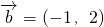 ,
,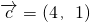 ,回答下列三个问题:
,回答下列三个问题:
(1)试写出将 用
用 ,
, 表示的表达式;
表示的表达式;
(2)若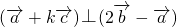 ,求实数k的值;
,求实数k的值;
(3)若向量 满足
满足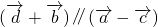 ,且
,且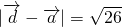 ,求
,求 .
.
解:(1)设 ,m,n∈R,
,m,n∈R,
则(3,2)=m(-1,2)+n(4,1),即 ,∴
,∴ ∴
∴ .
.
(2) ,
,
由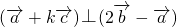 知,(-5)(3+4k)+2(2+k)=0∴
知,(-5)(3+4k)+2(2+k)=0∴ .
.
(3)设 ,x,y∈R
,x,y∈R
则 ,
,
由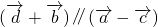 知,(x-1)+(y+2)=0,即x+y+1=0①
知,(x-1)+(y+2)=0,即x+y+1=0①
又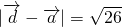 ,即(x-3)2+(y-2)2=26②
,即(x-3)2+(y-2)2=26②
联立①②,解得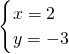 或
或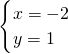 ∴
∴ 或
或 .
.
分析:(1)先设设 ,然后将坐标代入解二元一次方程组即可求出结果;
,然后将坐标代入解二元一次方程组即可求出结果;
(2)首先表示出向量,然后利用两个向量共线的条件x1•y2-x2•y1=0.
(3)利用两个向量共线的条件x1•y2-x2•y1=0 及且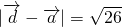 ,解出向量
,解出向量  的坐标.
的坐标.
点评:本题考查向量共线的条件及向量的模的概念,熟练掌握向量平行的条件,属于基础题.
 ,m,n∈R,
,m,n∈R,则(3,2)=m(-1,2)+n(4,1),即
 ,∴
,∴ ∴
∴ .
.(2)
 ,
,
由
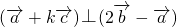 知,(-5)(3+4k)+2(2+k)=0∴
知,(-5)(3+4k)+2(2+k)=0∴ .
.(3)设
 ,x,y∈R
,x,y∈R则
 ,
,
由
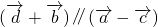 知,(x-1)+(y+2)=0,即x+y+1=0①
知,(x-1)+(y+2)=0,即x+y+1=0①又
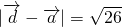 ,即(x-3)2+(y-2)2=26②
,即(x-3)2+(y-2)2=26②联立①②,解得
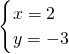 或
或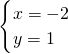 ∴
∴ 或
或 .
.分析:(1)先设设
 ,然后将坐标代入解二元一次方程组即可求出结果;
,然后将坐标代入解二元一次方程组即可求出结果;(2)首先表示出向量,然后利用两个向量共线的条件x1•y2-x2•y1=0.
(3)利用两个向量共线的条件x1•y2-x2•y1=0 及且
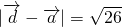 ,解出向量
,解出向量  的坐标.
的坐标.点评:本题考查向量共线的条件及向量的模的概念,熟练掌握向量平行的条件,属于基础题.

练习册系列答案
相关题目