Question

如图，已知在60°的二面角α—l—β中，A∈α,B∈β，AC⊥l于C，BD⊥l于D，并且AC=2，BD=4，AB=10.求：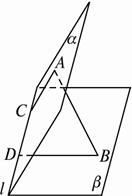

(1)CD的长度；

(2)AB和棱l所成的角的余弦值.

Answer 1

解：(1)∵AC⊥l,BD⊥l,α—l—β为60°的二面角,∴〈,〉=60°.?

∵=++,?

∴²=²+²+²+2+2+2.?

∴10²=2²+²+4²+2||||cos〈,〉.?

∴²=80-2×2×4×cos120°=88.?

∴CD的长度为2.?

(2)∵=(++) =+²+=²=88.?

∴cos〈,〉===.

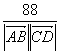点评：运用向量求线段长，一般是把这条线段“向量化”，通过计算向量的模求得线段长.运用向量求两线段的夹角(或直线夹角)，也需要把线段“向量化”，通过计算两向量的数量积与两向量的模的积，再求其商得夹角余弦.