题目内容
已知函数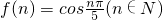 ,则
,则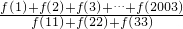 的值为
的值为
- A.1
- B.
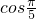
- C.

- D.2
A
分析:先通过诱导公式找到规律,f(1)+f(2)+f(3)+f(4)=(cos +cos
+cos )+(cos
)+(cos +cos
+cos )=-(cos
)=-(cos +cos
+cos )+(cos
)+(cos +cos
+cos )=0,然后再利用诱导公式及周期性求解.
)=0,然后再利用诱导公式及周期性求解.
解答:∵f(1)+f(2)+f(3)+f(4)=(cos +cos
+cos )+(cos
)+(cos +cos
+cos )
)
=-(cos +cos
+cos )+(cos
)+(cos +cos
+cos )=0,f(5)=cosπ=-1;
)=0,f(5)=cosπ=-1;
f(6)+f(7)+f(8)+f(9)=cos(π+ )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )
)
=-(cos +cos
+cos +cos
+cos +cos
+cos )
)
=-[f(1)+f(2)+f(3)+f(4)]=0,f(10)=cos2π=1;
∴f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)+f(8)+f(9)+f(10)=0
函数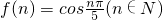 的周期T=
的周期T=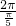 =10,因此从f(1)起,每连续10项的和等于0,
=10,因此从f(1)起,每连续10项的和等于0,
∴f(1)+f(2)+f(3)+…f(2003)=f(2001)+f(2002)+f(2003)
=f(1)+f(2)+f(3)=cos +cos
+cos +cos
+cos =cos
=cos
f(11)+f(22)+f(33)=f(1)+f(2)+f(3)=cos +cos
+cos +cos
+cos =cos
=cos
∴原式=1
故选A.
点评:本题主要考查函数的规律的探索,学习三角函数关键是熟练应用相关公式,将问题进行转化.
分析:先通过诱导公式找到规律,f(1)+f(2)+f(3)+f(4)=(cos
 +cos
+cos )+(cos
)+(cos +cos
+cos )=-(cos
)=-(cos +cos
+cos )+(cos
)+(cos +cos
+cos )=0,然后再利用诱导公式及周期性求解.
)=0,然后再利用诱导公式及周期性求解.解答:∵f(1)+f(2)+f(3)+f(4)=(cos
 +cos
+cos )+(cos
)+(cos +cos
+cos )
)=-(cos
 +cos
+cos )+(cos
)+(cos +cos
+cos )=0,f(5)=cosπ=-1;
)=0,f(5)=cosπ=-1;f(6)+f(7)+f(8)+f(9)=cos(π+
 )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )+cos(π+
)+cos(π+ )
)=-(cos
 +cos
+cos +cos
+cos +cos
+cos )
)=-[f(1)+f(2)+f(3)+f(4)]=0,f(10)=cos2π=1;
∴f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)+f(8)+f(9)+f(10)=0
函数
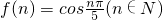 的周期T=
的周期T=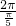 =10,因此从f(1)起,每连续10项的和等于0,
=10,因此从f(1)起,每连续10项的和等于0,∴f(1)+f(2)+f(3)+…f(2003)=f(2001)+f(2002)+f(2003)
=f(1)+f(2)+f(3)=cos
 +cos
+cos +cos
+cos =cos
=cos
f(11)+f(22)+f(33)=f(1)+f(2)+f(3)=cos
 +cos
+cos +cos
+cos =cos
=cos
∴原式=1
故选A.
点评:本题主要考查函数的规律的探索,学习三角函数关键是熟练应用相关公式,将问题进行转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则 的值为( )
的值为( ) C.-1 D.4
C.-1 D.4 ,则
,则 的值为
的值为  ,则
,则 的值为
的值为 B.9 C.
B.9 C. 9 D.
9 D.
 ,则
,则 的值为( )
的值为( ) B. 1 C.
B. 1 C.  D.2
D.2 ,则
,则