题目内容
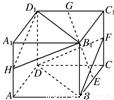
已知如图：E、F、G、H分别是正方体ABCD－A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.
(1)求证：EG∥平面BB1D1D；
(2)求证：平面BDF∥平面B1D1H.
(1)取B1D1的中点O，连接GO，OB，易证四边形BEGO为平行四边形，故OB∥GE，
由线面平行的判定定理即可证EG∥平面BB1D1D.
(2)由题意可知BD∥B1D1.
如图，连接HB、D1F，
易证四边形HBFD1是平行四边形，
故HD1∥BF.
又B1D1∩HD1＝D1，
BD∩BF＝B，
所以平面BDF∥平面B1D1H.
练习册系列答案
小学教材完全解读系列答案
相关题目
10、已知如图：E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点．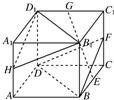
已知如图：E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点．
