题目内容
平面直角坐标系中,点集M={(x,y)|
α,β∈R},则点集M所覆盖的平面图形的面积为( )
|
| A、4π |
| B、3π |
| C、2π |
| D、与α,β有关 |
分析:欲求点集M所覆盖的平面图形的面积,先看点M的轨迹是什么图形才行,将x,y的式子平方相加后即可得出x2+y2=2+2sin(α-β).再结合三角函数的有界性即可解决问题.
解答:解:∵
两式平方相加得:
x2+y2=1+1+2sinαcosβ-2cosαsinβ
即:x2+y2=2+2sin(α-β).
由于-1≤sin(α-β)≤1,
∴0≤2+2sin(α-β)≤4,
∴随着α-β 的变化,方程x2+y2=2+2sin(α-β)圆心在(0,0),半径最大为2的圆,
点集M所覆盖的平面图形的面积为:2×2×π=4π.
故选A.
|
两式平方相加得:
x2+y2=1+1+2sinαcosβ-2cosαsinβ
即:x2+y2=2+2sin(α-β).
由于-1≤sin(α-β)≤1,
∴0≤2+2sin(α-β)≤4,
∴随着α-β 的变化,方程x2+y2=2+2sin(α-β)圆心在(0,0),半径最大为2的圆,
点集M所覆盖的平面图形的面积为:2×2×π=4π.
故选A.
点评:本题是考查参数方程化成普通方程,本题主要考查了圆的标准方程,属于基础题.

练习册系列答案
相关题目
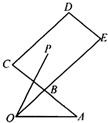 如图,B是AC的中点,
如图,B是AC的中点, 在平面直角坐标系中,点P(x,y)满足约束条件:
在平面直角坐标系中,点P(x,y)满足约束条件: