题目内容
已知非零向量 、
、 满足|a|=1,且
满足|a|=1,且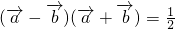 .
.
(1)求| |;
|;
(2)当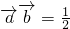 时,求向量a
时,求向量a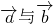 的夹角θ的值.
的夹角θ的值.
解:(1)因为 ,即
,即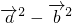 =
= ,
,
所以 ,故
,故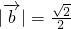 .
.
(2)因为cosθ= =
= ,又0≤θ<180°,故θ=45°
,又0≤θ<180°,故θ=45°
分析:(1)由题意可得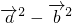 =
= ,故
,故  .
.
(2)利用两个向量夹角公式可得饿cosθ= =
= ,又0≤θ<180°,求得θ 的值.
,又0≤θ<180°,求得θ 的值.
点评:本题考查两个向量的数量积的定义,向量的模的定义,求向量的模的方法,两个向量夹角公式的应用,求出| |的
|的
值,是解题的关键.
 ,即
,即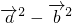 =
= ,
,所以
 ,故
,故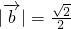 .
. (2)因为cosθ=
 =
= ,又0≤θ<180°,故θ=45°
,又0≤θ<180°,故θ=45°分析:(1)由题意可得
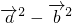 =
= ,故
,故  .
.(2)利用两个向量夹角公式可得饿cosθ=
 =
= ,又0≤θ<180°,求得θ 的值.
,又0≤θ<180°,求得θ 的值.点评:本题考查两个向量的数量积的定义,向量的模的定义,求向量的模的方法,两个向量夹角公式的应用,求出|
 |的
|的值,是解题的关键.

练习册系列答案
相关题目
 )·
)·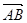 与
与 满足(
满足(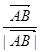 +
+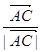 )·
)· =0,且
=0,且
 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为
的夹角为 B.
B. C.
C. D.
D.
 和
和 满足
满足 ,且
,且 ,
,