题目内容
(本小题14分)
在等差数列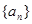 中,
中,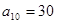 ,
, .
.
(1)求数列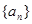 的通项
的通项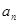 ;
;
(2)令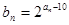 ,证明:数列
,证明:数列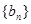 为等比数列;
为等比数列;
(3)求数列 的前
的前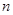 项和
项和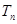 .
.
(1) ;
;
(2)见解析
(3) 

解析试题分析:(1)先由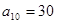 ,
, ,可建立关于a1和d的方程求出a1和d的值,从而求出通项
,可建立关于a1和d的方程求出a1和d的值,从而求出通项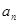 .
.
(2)再(1)的基础上可求出 ,再利用等比数列的定义可判断出
,再利用等比数列的定义可判断出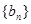 为等比数列;
为等比数列;
(3)由于 的通项为
的通项为 显然要采用错位相减的方法求和。
显然要采用错位相减的方法求和。
(1)设数列 首项为
首项为 ,公差为
,公差为
依题意得 ,………2分
,………2分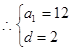 ………………3分
………………3分 ……………4分
……………4分
(2)
 是以
是以 =4为首项,4为公比的等比数列。………………………8分
=4为首项,4为公比的等比数列。………………………8分
(3) ……………………9分
……………………9分 …………………11分
…………………11分
考点:等差数列的通项公式,等比数列的定义及通项公式及其前n项和公式,错位相减法求和。
点评:等差数列及等比数列的定义是判断数列是否是等差或等比数列的依据,并且要注意结合通项公式的特点判断选用何种方法求和,本题是一个等差数列与一个等比数列的积所以应采用错位相减法求和.

练习册系列答案
相关题目
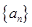 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列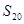 .
.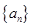 中,
中,  ,
, ,
, .
. 是等比数列;
是等比数列; 项和
项和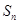 .
. 成立.
成立. 满足:
满足: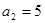 ,
,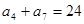 ,
,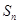 .
.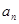 及前n项和
及前n项和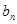 =
=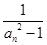 (n
(n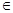 N*),求数列
N*),求数列 的前n项和
的前n项和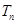 .
.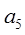 =10,且
=10,且 是等比数列{
是等比数列{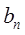 }的第1,3,5项,且
}的第1,3,5项,且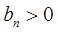 .
. }的第20项,(2)求数列{
}的第20项,(2)求数列{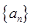 满足:
满足: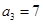 ,
, ,
,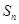 .
.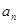 及
及 (
( ),求数列
),求数列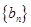 的前n项和
的前n项和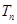 .
. =9a2a6.
=9a2a6. 的前n项和Tn;
的前n项和Tn; ≥ (7? 2n)Tn恒成立的实数k 的取值范围.
≥ (7? 2n)Tn恒成立的实数k 的取值范围. 的前
的前 项和为
项和为 ,
, (
( ).
).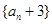 是等比数列,求出数列
是等比数列,求出数列 ,求数列
,求数列 的前
的前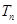 ;
;
 ,
,
 哪一个最大?并求出最大值
哪一个最大?并求出最大值