题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}a•{2^x}(x≤0)\\{log_2}x(x>0)\end{array}$,若关于x的方程f[f(x)]=0有且只有一个实数根,则实数a的取值范围是( )| A. | (-∞,0) | B. | (-∞,0)∪(0,1) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
分析 利用换元法设f(x)=t,则方程等价为f(t)=0,根据指数函数和对数函数图象和性质求出t=1,利用数形结合进行求解即可.
解答 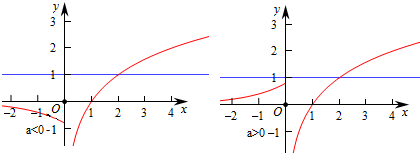 解:令f(x)=t,则方程f[f(x)]=0等价为f(t)=0,
解:令f(x)=t,则方程f[f(x)]=0等价为f(t)=0,
由选项知a≠0,
当a>0时,当x≤0,f(x)=a•2x>0,
当x>0时,由f(x)=log2x=0得x=1,
即t=1,作出f(x)的图象如图:
若a<0,则t=1与y=f(x)只有一个交点,恒满足条件,
若a>0,要使t=1与y=f(x)只有一个交点,
则只需要当x≤0,t=1与f(x)=a•2x,没有交点,
即此时f(x)=a•2x<1,
即f(0)<1,
即a•20<1,
解得0<a<1,
综上0<a<1或a<0,
即实数a的取值范围是(-∞,0)∪(0,1),
故选:B.
点评 本题主要考查函数方程根的个数的应用,利用换元法求出t=1是解决本题的关键.注意利用指数函数和对数函数的图象,结合数形结合是解决本题的关键.综合性较强.

练习册系列答案
相关题目
4.已知函数f(x)=x3-3x2+a,若f(x+1)是奇函数,则曲线y=f(x)在点(0,a)处的切线方程是( )
| A. | x=0 | B. | x=2 | C. | y=2 | D. | y=4 |
3.设x0是函数f(x)=2x-|log2x|-1的一个零点,若a>x0,则f(a)满足( )
| A. | f(a)>0 | B. | f(a)<0 | ||
| C. | f(a)可以等于0 | D. | f(a)的符号不能确定 |
4.已知复数z=3-2i-$\frac{5i}{2-i}$,则复数z对应复平面上的点Z位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
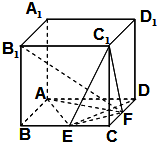 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,