题目内容
 如图,在三棱锥P-ABC中,∠PAB=∠PAC=∠ACB=90°.
如图,在三棱锥P-ABC中,∠PAB=∠PAC=∠ACB=90°.(Ⅰ)求证:平面PBC⊥平面PAC;
(Ⅱ)若PA=1,AB=2,当三棱锥P-ABC的体积最大时,在线段AC上是否存在一点D,使得直线BD与平面PBC所成角为30°?若存在,求出CD的长;若不存在,说明理由.(参考公式:棱锥的体积公式V=
| 1 | 3 |
分析:(I)由∠PAB=∠PAC=90°,可得PA⊥AB,PA⊥AC.进而由线面垂直的判定定理得到PA⊥平面ABC,进而BC⊥PA,再由∠ACB=90°及线面垂直的判定定理得到BC⊥平面PAC,再由面面垂直的判定定理可得平面PBC⊥平面PAC;
(Ⅱ)由已知及(Ⅰ)所证可知,PA⊥平面ABC,BC⊥CA,即PA是三棱锥P-ABC的高.求出满足条件三棱锥P-ABC的体积最大时∠ABC的大小,以C为原点,建立如图的空间直角坐标系C-xyz,设线段AC上的点D的坐标为D(t,0,0),进而求出满足条件的t值,进而可得结论.
(Ⅱ)由已知及(Ⅰ)所证可知,PA⊥平面ABC,BC⊥CA,即PA是三棱锥P-ABC的高.求出满足条件三棱锥P-ABC的体积最大时∠ABC的大小,以C为原点,建立如图的空间直角坐标系C-xyz,设线段AC上的点D的坐标为D(t,0,0),进而求出满足条件的t值,进而可得结论.
解答:证明:(Ⅰ)∵∠PAB=∠PAC=90°,
∴PA⊥AB,PA⊥AC.
∵AB∩AC=A,AB,AC?平面ABC
∴PA⊥平面ABC------------------------(1分)
∵BC?平面ABC,
∴BC⊥PA.------------------------(2分)
∵∠ACB=90°,
∴BC⊥CA.
∵PA∩CA=A,PA,CA?平面PAC
∴BC⊥平面PAC.------------(3分)
∵BC?平面PBC,
∴平面PBC⊥平面PAC.------------(4分)
(Ⅱ)由已知及(Ⅰ)所证可知,PA⊥平面ABC,BC⊥CA,
∴PA是三棱锥P-ABC的高.
∵PA=1,AB=2,∠ACB=90°,
设∠ABC=θ(0<θ<
),
则BC=ABcosθ=2cosθ,AC=ABsinθ=2sinθ.
S△ABC=
×2cosθ×2sinθ=sin2θ,
∴VP-ABC=
S△ABC×PA=
sin2θ------(6分)
∴当θ=
,VP-ABC有最大值
,
此时BC=2cos
=
.------------(7分)
以C为原点,建立如图的空间直角坐标系C-xyz,
则
=(0,
,0),
=(
,0,1),
设
=(x,y,z)是平面PBC的法向量,

则
⇒
,
取x=1,得
=(1,0,-
),------------(9分)
设线段AC上的点D的坐标为D(t,0,0),
则
=(t,-
,0)(0≤t≤
),
∵sin30°=
=
,
解得t=
∉[0,
],------------(11分)
∴在线段AC上不存在点D,使得直线BD与平面PBC所成角为30°.------------(12分)
∴PA⊥AB,PA⊥AC.
∵AB∩AC=A,AB,AC?平面ABC
∴PA⊥平面ABC------------------------(1分)
∵BC?平面ABC,
∴BC⊥PA.------------------------(2分)
∵∠ACB=90°,
∴BC⊥CA.
∵PA∩CA=A,PA,CA?平面PAC
∴BC⊥平面PAC.------------(3分)
∵BC?平面PBC,
∴平面PBC⊥平面PAC.------------(4分)
(Ⅱ)由已知及(Ⅰ)所证可知,PA⊥平面ABC,BC⊥CA,
∴PA是三棱锥P-ABC的高.
∵PA=1,AB=2,∠ACB=90°,
设∠ABC=θ(0<θ<
| π |
| 2 |
则BC=ABcosθ=2cosθ,AC=ABsinθ=2sinθ.
S△ABC=
| 1 |
| 2 |
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
∴当θ=
| π |
| 4 |
| 1 |
| 3 |
此时BC=2cos
| π |
| 4 |
| 2 |
以C为原点,建立如图的空间直角坐标系C-xyz,
则
| CB |
| 2 |
| CP |
| 2 |
设
| n |

则
|
|
取x=1,得
| n |
| 2 |
设线段AC上的点D的坐标为D(t,0,0),
则
| BD |
| 2 |
| 2 |
∵sin30°=
|
| ||||
|
|
| t | ||||
|
解得t=
| 6 |
| 2 |
∴在线段AC上不存在点D,使得直线BD与平面PBC所成角为30°.------------(12分)
点评:本题考查的知识点是直线与平面所成的角,棱锥的体积,平面与平面垂直的判定,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
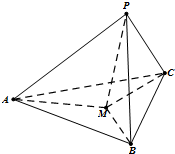 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是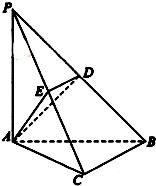 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱