题目内容
10.设集合A={(x,y)|y≥|x-1|},B={(x,y)|-2y+2≥0},C={(x,y)|ax-y+a≥0},若(A∩B)⊆C,则实数a的最小值为1.分析 根据集合中的条件确定各集合对应的平面区域,再由集合间的包含关系,得出a的最小值.
解答 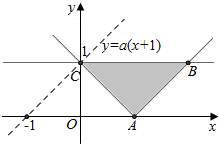 解:对于集合A,A={(x,y)|y≥|x-1|},
解:对于集合A,A={(x,y)|y≥|x-1|},
表示的是,函数y=|x-1|图象上方的部分,
对于集合B,B={(x,y)|-2y+2≥0},
表示的是,直线y=1下方的部分,
所以,A∩B表示的区域就是如图阴影(△ABC),
再考察集合C,y≤a(x+1),
表示的是直线y=a(x+1)下方的部分,
且该直线过定点(-1,0),如图虚线,
要使(A∩B)⊆C,则直线y=a(x+1)的斜率k≥1,
而k=a,所以,a≥1,
即实数a的最小值为1,
故答案为:1.
点评 本题主要考查了集合间交集,子集及其运算,以及直线的斜率与区域之间的关联,属于中档题.

练习册系列答案
相关题目
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz 中,
中, ,
, 为数列
为数列 项和,则
项和,则
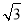 B.2 C.
B.2 C.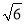 D.3
D.3