题目内容
下面有四个命题：
①函数y=sin(2x-
)的一条对称轴为x=
；
②把函数y=3sin(2x+
)的图象向右平移
个单位长度得到y=3sin2x的图象．
③存在角α．使得sinα+cosα=
；
④对于任意锐角α，β都有sin（α+β）＜sinα+sinβ．
其中，正确的是
①函数y=sin(2x-
| π |
| 3 |
| 5π |
| 12 |
②把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
③存在角α．使得sinα+cosα=
| 3 |
④对于任意锐角α，β都有sin（α+β）＜sinα+sinβ．
其中，正确的是
①②④
①②④
．（只填序号）分析：根据对称轴对应的函数值是最值，可以判断①的真假；根据正弦函数的图象的平移的大小和方向，可以判断②的真假；根据三角函数中正弦函数的最值，可以判断③的真假；根据锐角的三角函数值与1的关系，可以判断④的真假；进而得到答案．
解答：解：要验证函数y=sin(2x-
)的一条对称轴为x=
，
只要把所给的对称轴代入得到y=sin（2×
-
）=sin
=1，故①正确；
把 y=3sin(2x+
)=3sin[2（x+
）]的图象向右平移
得到y=3sin2x的图象，故②正确；
sinα+cosα=
sin(α+
)，最大值是
，不存在角α使得sinα+cosα=
，故③不正确；
sin（α+β）=sinαcosβ+cosαsinβ，
当对于锐角α，β有cosα＜1，cosβ＜1，故有sin（α+β）＜sinα+sinβ，故④正确，
综上可知①②④正确，
故答案为：①②④
| π |
| 3 |
| 5π |
| 12 |
只要把所给的对称轴代入得到y=sin（2×
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
把 y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
sinα+cosα=
| 2 |
| π |
| 4 |
| 2 |
| 3 |
sin（α+β）=sinαcosβ+cosαsinβ，
当对于锐角α，β有cosα＜1，cosβ＜1，故有sin（α+β）＜sinα+sinβ，故④正确，
综上可知①②④正确，
故答案为：①②④
点评：本题考查命题的真假判断及其应用，正弦函数的对称性，正弦函数的性质最值，图象的平移变换，本题解题的关键是熟练掌握三角函数的基础知识，可以判断出题目中4个命题的真假，本题是一个中档题目．
练习册系列答案
相关题目
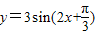的图象向右平移
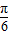得y=3sin2x的图象；
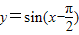在（0，π）上是减函数．