题目内容
设函数f(x)=x2ex-1+ax3+bx2,已知x=-2和x=1为f(x)的极值点。
(1)求a和b的值;
(2)讨论f(x)的单调性;
(3)设 g(x)= x3-x2,试比较f(x)与g(x)的大小。
x3-x2,试比较f(x)与g(x)的大小。
(1)求a和b的值;
(2)讨论f(x)的单调性;
(3)设 g(x)=
 x3-x2,试比较f(x)与g(x)的大小。
x3-x2,试比较f(x)与g(x)的大小。解:(1)因为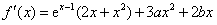
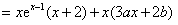 ,
,
又 和
和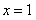 为
为 的极值点,
的极值点,
所以 ,
,
因此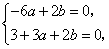
解方程组得 ,
,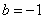 。
。
(2)因为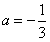 ,
, ,
,
所以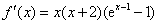 ,
,
令 ,
,
解得 ,
,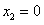 ,
,
因为当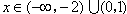 时,
时, ;
;
当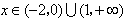 时,
时,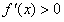
所以 在
在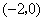 和
和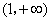 上是单调递增的;
上是单调递增的;
在 和
和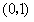 上是单调递减的。
上是单调递减的。
(3)由(1)可知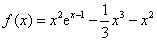 ,
,
故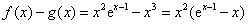 ,
,
令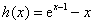 ,
,
则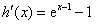
令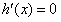 ,得
,得 ,
,
因为 时,
时,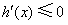 ,
,
所以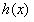 在
在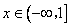 上单调递减
上单调递减
故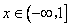 时,
时,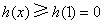 ;
;
因为 时,
时,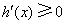 ,
,
所以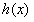 在
在 上单调递增
上单调递增
故 时,
时,
所以对任意 ,恒有
,恒有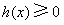 ,
,
又 ,
,
因此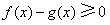 ,
,
故对任意 ,恒有
,恒有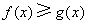 。
。
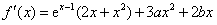
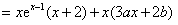 ,
,又
 和
和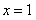 为
为 的极值点,
的极值点,所以
 ,
,因此
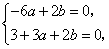
解方程组得
 ,
,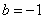 。
。(2)因为
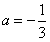 ,
, ,
,所以
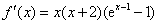 ,
,令
 ,
,解得
 ,
,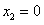 ,
,
因为当
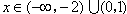 时,
时, ;
;当
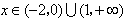 时,
时,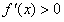
所以
 在
在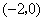 和
和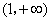 上是单调递增的;
上是单调递增的;在
 和
和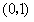 上是单调递减的。
上是单调递减的。(3)由(1)可知
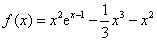 ,
,故
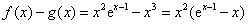 ,
,令
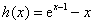 ,
,则
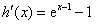
令
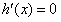 ,得
,得 ,
,因为
 时,
时,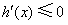 ,
,所以
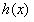 在
在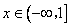 上单调递减
上单调递减故
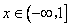 时,
时,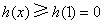 ;
;因为
 时,
时,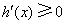 ,
,所以
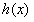 在
在 上单调递增
上单调递增故
 时,
时,
所以对任意
 ,恒有
,恒有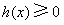 ,
,又
 ,
,因此
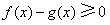 ,
,故对任意
 ,恒有
,恒有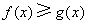 。
。
练习册系列答案
相关题目