题目内容
已知（
+
)n的展开式中，前三项系数成等差数列,(1)求展开式的中间项;
(2)求展开式中x的有理项.
解:前三项的系数依次为1、、
，由题设得2·
=1+
,即n2-9n+8=0.解之,得n=8或n=1（舍去）.
(1)由n=8知展开式共有9项，中间项为第5项，它是T5=
(
)4(
)8-4.
(2)展开式中第r+1项为Tr+1=
(
)8-r(
)r=
(
)r，要使Tr+1项为x的有理项，则
r应为整数，即r是4的倍数.
又∵0≤r≤8,∴r=0,4,8.故展开式中x的有理项为第1,5,9项,即T1=
x4,T5=
x,T9=
x-2.
练习册系列答案
相关题目
)n的展开式中，第6项为常数项.
)n的展开式中第三项与第五项的系数之比为
,则展开式中常数项是( )
)n的展开式的第三项与第二项的系数的比为11∶2，则n是( )
)n的展开式的常数项是第7项，则正整数n的值为 （ ）
－
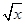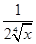)n的展开式中，前三项系数的绝对值依次成等差数列．(1)证明：展开式中没有常数项；