题目内容
设各项均为正数的数列{an}的前n项和为Sn,已知2a2=a1+a3,数列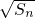 是公差为d的等差数列,则数列{an}的通项公式为________.(用n,d表示).
是公差为d的等差数列,则数列{an}的通项公式为________.(用n,d表示).
(2n-1)d2
分析:根据等差数列的通项公式,结合已知,列出关于a1、d的方程,求出a1,进而推出sn,再利用an与sn的关系求出an.
解答:由题意知:d>0,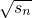 =
=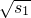 +(n-1)d=
+(n-1)d=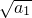 +(n-1)d,又2a2=a1+a3,
+(n-1)d,又2a2=a1+a3,
∴3a2=S3,即3(S2-S1)=S3,
∴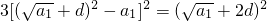 ,
,
化简得: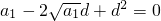 ,化简可得
,化简可得 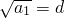 ,即
,即  .
.
∴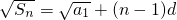 =d+(n-1)d=nd,∴
=d+(n-1)d=nd,∴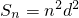 .
.
当n≥2时,an=Sn-Sn-1=n2d2-(n-1)2d2=(2n-1)d2,也适合n=1情形,故所求an=(2n-1)d2 .
故答案为(2n-1)d2.
点评:本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力.
分析:根据等差数列的通项公式,结合已知,列出关于a1、d的方程,求出a1,进而推出sn,再利用an与sn的关系求出an.
解答:由题意知:d>0,
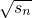 =
=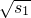 +(n-1)d=
+(n-1)d=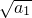 +(n-1)d,又2a2=a1+a3,
+(n-1)d,又2a2=a1+a3,∴3a2=S3,即3(S2-S1)=S3,
∴
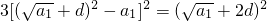 ,
,化简得:
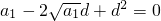 ,化简可得
,化简可得 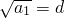 ,即
,即  .
.∴
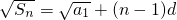 =d+(n-1)d=nd,∴
=d+(n-1)d=nd,∴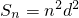 .
.当n≥2时,an=Sn-Sn-1=n2d2-(n-1)2d2=(2n-1)d2,也适合n=1情形,故所求an=(2n-1)d2 .
故答案为(2n-1)d2.
点评:本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力.

练习册系列答案
相关题目