题目内容
(本小题14分)
已知函数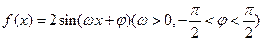 的图像如图所示,直线
的图像如图所示,直线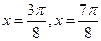 是其两条对称轴。
是其两条对称轴。
(1)求函数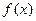 的解析式并写出函数的单调增区间;
的解析式并写出函数的单调增区间;
(2)若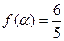 ,且
,且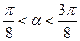 ,求
,求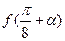 的值。
的值。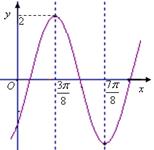
已知函数
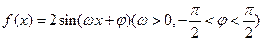 的图像如图所示,直线
的图像如图所示,直线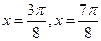 是其两条对称轴。
是其两条对称轴。(1)求函数
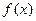 的解析式并写出函数的单调增区间;
的解析式并写出函数的单调增区间;(2)若
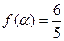 ,且
,且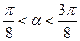 ,求
,求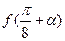 的值。
的值。
(1)函数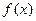 的单调增区间为
的单调增区间为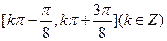
(2)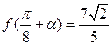
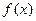 的单调增区间为
的单调增区间为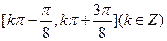
(2)
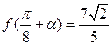
(1)由题意,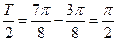 ,∴
,∴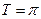 ,
,
又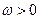 ,故
,故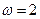 ,∴
,∴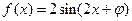 , ……………………2分
, ……………………2分
由 ,解得
,解得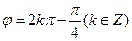 ,
,
又 ,∴
,∴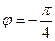 ,∴
,∴ 。 ……………………5分
。 ……………………5分
由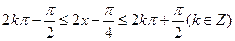 知,
知,
∴函数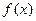 的单调增区间为
的单调增区间为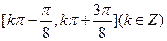 。 ……………7分
。 ……………7分
(2)解法1:依题意得: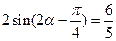 ,即
,即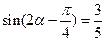 , ……………8分
, ……………8分
∵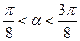 ,∴
,∴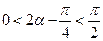 ,
,
∴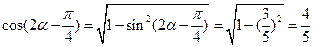 , ……………………10分
, ……………………10分
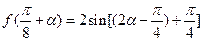
∵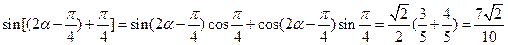
∴ 。 ……………………14分
。 ……………………14分
解法2:依题意得: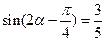 ,得
,得 ,① ………………9分
,① ………………9分
∵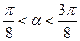 ,∴
,∴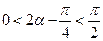 ,
,
∴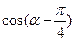 =
= , ……………………11分
, ……………………11分
由 得
得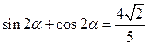 -----------②
-----------②
①+②得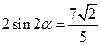 ,
,
∴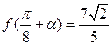 ……………………14分
……………………14分
解法3:由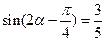 得
得 , ……………………9分
, ……………………9分
两边平方得
 ,
,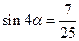 ,
,
∵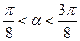 ∴
∴ ,
,
∴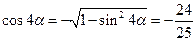 , ……………………11分
, ……………………11分
∴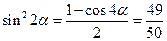 ,又
,又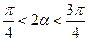 ,∴
,∴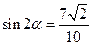 ,
,
∴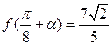 。 ……………………14分
。 ……………………14分
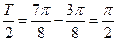 ,∴
,∴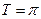 ,
,又
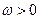 ,故
,故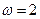 ,∴
,∴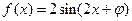 , ……………………2分
, ……………………2分由
 ,解得
,解得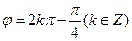 ,
,又
 ,∴
,∴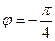 ,∴
,∴ 。 ……………………5分
。 ……………………5分由
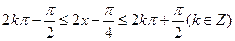 知,
知,
∴函数
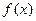 的单调增区间为
的单调增区间为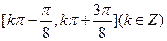 。 ……………7分
。 ……………7分(2)解法1:依题意得:
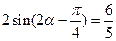 ,即
,即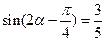 , ……………8分
, ……………8分∵
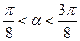 ,∴
,∴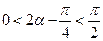 ,
,∴
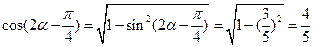 , ……………………10分
, ……………………10分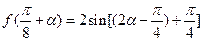
∵
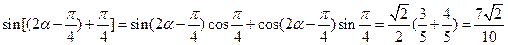
∴
 。 ……………………14分
。 ……………………14分解法2:依题意得:
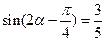 ,得
,得 ,① ………………9分
,① ………………9分∵
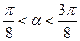 ,∴
,∴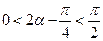 ,
,∴
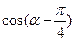 =
= , ……………………11分
, ……………………11分由
 得
得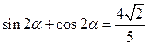 -----------②
-----------②①+②得
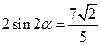 ,
,∴
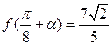 ……………………14分
……………………14分解法3:由
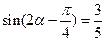 得
得 , ……………………9分
, ……………………9分两边平方得

 ,
,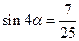 ,
,∵
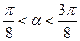 ∴
∴ ,
,∴
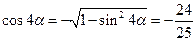 , ……………………11分
, ……………………11分∴
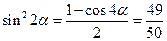 ,又
,又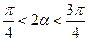 ,∴
,∴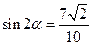 ,
,∴
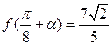 。 ……………………14分
。 ……………………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,sin
,sin ,求角
,求角 求
求 的值.
的值.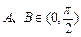 ,若
,若
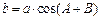 .
.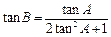 ;
;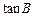 取最大值时,求
取最大值时,求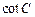 的值.
的值.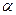 的顶点在原点,始边与
的顶点在原点,始边与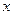 轴非负半轴重合,终边为射线
轴非负半轴重合,终边为射线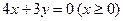 ,则
,则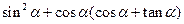 的值是
的值是
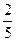
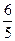
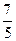
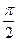 的是:( )
的是:( )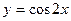
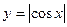
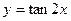
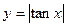
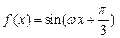 (
(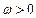 )的最小正周期为
)的最小正周期为 ,则该函数的图象
,则该函数的图象 ,0)对称
,0)对称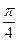 ,0)对称
,0)对称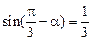 ,则
,则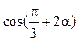 =_________.
=_________.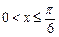 时,函数
时,函数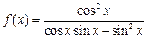 的最小值为_________________.
的最小值为_________________.