题目内容
(本小题满分12分)已知函数 .
.
(1)求函数 在点
在点 处的切线方程;
处的切线方程;
(2)若方程 有唯一解,试求实数
有唯一解,试求实数 的值.
的值.
(1) ;(2)
;(2)
【解析】
试题分析:(1)求 ,由导数的几何意义可知切线的斜率
,由导数的几何意义可知切线的斜率 ,再求
,再求 可得切点.根据点斜式可得切线方程.(2)
可得切点.根据点斜式可得切线方程.(2)
 .即
.即 .令
.令 ,求导.讨论导数的符号.导数正得增区间导数负得减区间.根据单调性可求函数
,求导.讨论导数的符号.导数正得增区间导数负得减区间.根据单调性可求函数 在
在 上的最值.根据数形结合分析可得
上的最值.根据数形结合分析可得 的值.
的值.
试题解析:解 (1)因为 ,所以切线的斜率
,所以切线的斜率 .
.
又f(1)=1,故所求的切线方程为 .即
.即 .
.
(2)原方程等价于 ,
,
令 ,则原方程即为
,则原方程即为 .
.
因为当 时原方程有唯一解,所以函数
时原方程有唯一解,所以函数 与
与 的图象在
的图象在 轴右侧有唯一的交点.
轴右侧有唯一的交点.
又 ,且
,且 ,
,
所以当 时,
时, ;当
;当 时,
时, .
.
即 在
在 上单调递增,在(0,4)上单调递减,故
上单调递增,在(0,4)上单调递减,故 在x=4处取得最小值,
在x=4处取得最小值,
又 且
且 无限趋近0时,
无限趋近0时, 无限趋近正无穷大,
无限趋近正无穷大, 无限趋近正无穷大时,
无限趋近正无穷大时, 也无限趋近正无穷大
也无限趋近正无穷大
从而当 时原方程有唯一解的充要条件是
时原方程有唯一解的充要条件是 .
.
考点:1导数的几何意义;2用导数研究函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域是( )
的定义域是( ) B.
B. C.
C. D.
D.
 的值为2,则输出的
的值为2,则输出的 的值为
的值为
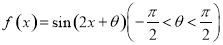 的图象向右平移
的图象向右平移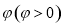 个单位长度后得到函数
个单位长度后得到函数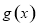 的图象,若
的图象,若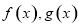 的图象都经过点
的图象都经过点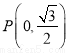 ,则
,则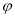 的值可以是
的值可以是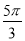 B.
B.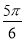 C.
C.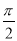 D.
D.
 ,则
,则
 B.
B.
 D.
D.
 在
在 内有定义,下列函数:
内有定义,下列函数: ;
;  ;
;  ;
; 中必为奇函数的有 .
中必为奇函数的有 .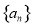 是等差数列,则下列数列中仍为等差数列的个数有 ( )
是等差数列,则下列数列中仍为等差数列的个数有 ( )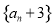 , ②
, ②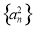 , ③
, ③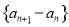 , ④
, ④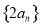 , ⑤
, ⑤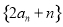 .
. 的定义域为
的定义域为 ,则函数
,则函数 的定义域是 .
的定义域是 .