题目内容
如图所示,已知正方体A1B1C1D1—ABCD的棱长为a.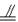
(1)求证:平面A1BD∥平面CB1D1;
(2)求平面A1BD与平面CB1D1的距离.
分析:利用面面平行的判定定理或推论,即可证明面面平行,寻找公垂线.
(1)证明:因为BB![]() DD1,
DD1,
所以四边形BDD1B1为平行四边形.
所以BD∥B1D1,BD![]() 平面CB1D1,B1D1
平面CB1D1,B1D1![]() 平面CB1D1,所以BD∥平面CB1D1.
平面CB1D1,所以BD∥平面CB1D1.
同理,A1D∥平面CB1D1.
又因为BD∩A1D=D,BD,A1D![]() 平面A1BD,
平面A1BD,
所以平面A1BD∥平面CB1D1.
(2)解:连结AC1,因为BD⊥AC,而AC是AC1在面AC上的投影.
由三垂线定理,知BD⊥AC1,同理A1B⊥AC1,
又BD∩A1B=B,所以AC1⊥平面A1BD.
同理AC1⊥平面CB1D1,设上,下底面对角线交点分别为O1,O.
连结A1O与AC1交于M,连结O1C与AC1交于N,则MN的长是平面A1BD和平面CB1D1的距离.
因为平面A1BD∥平面CB1D1,面AC1∩面A1BD=A1O,面AC1∩面CB1D1=O1C,
所以A1O∥O1C.
因为AO=OC,所以AM=MN.
同理MN=NC1
所以MN=![]() AC1=
AC1=![]()
![]()
=![]()
![]() ,
,
即平面A1BD与平面CB1D1的距离为![]() a.
a.
点拨:(1)求两个平行平面间的距离的一般步骤:一作图;二证明;三计算.
(2)求两个平行平面间的距离也可以转化为求点到面的距离.

练习册系列答案
相关题目
 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
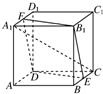
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.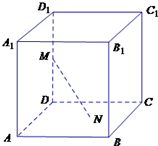 如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )
如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )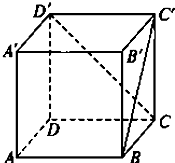 如图所示,已知正方体ABCD-A′B′C′D′,求:
如图所示,已知正方体ABCD-A′B′C′D′,求: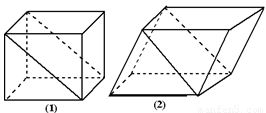
 的概率P1;
的概率P1; 的概率P2。
的概率P2。