题目内容
圆锥的轴截面是等腰直角三角形,如图所示,底面圆的半径为1,点O是圆心,过顶点S的截面SAB与底面所成的二面角是60°
(1)求截面SAB的面积;
(2)求点O到截面SAB的距离.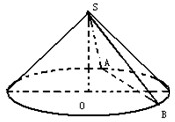
(1)求截面SAB的面积;
(2)求点O到截面SAB的距离.


(1)取AB中点C,
连接OC,SC,
则∠SCO=60°
SO=1,
所以OC=
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
∴截面SAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
(2)在Rt△SOC中,
作OD⊥SC,
则OD即为所求,
OD=
| SO×OC |
| SC |
1×
| ||||
|
| 1 |
| 2 |

练习册系列答案
相关题目
 求答下列三小题:
求答下列三小题:
 ),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.
),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.