题目内容
一个四面体的四个顶点在空间直角坐标系
中的坐标分别是（0，0，0），（1，2，0），（0，2，2），（3，0，1），则该四面体中以
平面为投影面的正视图的面积为
A． | B． | C． | D． |
A
解析试题分析：根据平行投影的知识可知:该四面体中以平面为投影面的正视图为一个上底为1，下底为2，高为2的直角梯形，所以面积为3.
考点：（1）空间直角坐标系；（2）平行投影三视图.
练习册系列答案
培优三好生系列答案
相关题目
为（ ）．
的侧棱长和底面边长均为
，且侧棱
底面
，其正视图是边长为
某几何体的三视图如图所示（单位：cm），则该几何体的体积是( )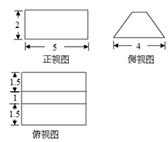
A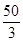．  | B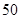． | C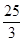． | D． |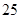
已知某个几何体的三视图如下，根据图中标出的尺寸（单位：
），则该几何体的体积是( )
A． | B． | C． | D． |
某几何体的三视图如图所示，则该几何体的体积为（ ）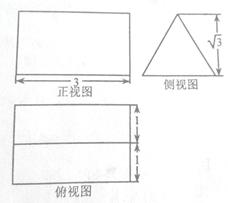
| A．6 | B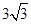． | C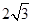． | D．3 |
如图所示,正方体ABCD
A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥PEFQ的体积( )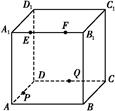
| A．与x,y都有关 |
| B．与x,y都无关 |
| C．与x有关,与y无关 |
| D．与y有关,与x无关 |
