题目内容
设动圆C与两圆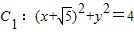
，
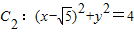中的一个内切，另一个外切．则动圆C的圆心M轨迹L的方程是 ．
【答案】分析：由题意直接利用已知列出关系式，结合圆锥曲线的定义，即可求出圆心M的轨迹方程．
解答：解：根据题意，有
，或
∴|MC1|-|MC2|=4＜|C1C2|=2
，或|MC2|-|MC1|=4＜|C1C2|=2
所以，圆心M的轨迹是以C1、C2为焦点的双曲线，
故M的轨迹方程为：
故答案为：
点评：本题考查曲线轨迹方程的求法，圆的几何性质的应用和圆锥曲线的定义是解决问题的关键，属基础题．
解答：解：根据题意，有
，或∴|MC1|-|MC2|=4＜|C1C2|=2
，或|MC2|-|MC1|=4＜|C1C2|=2所以，圆心M的轨迹是以C1、C2为焦点的双曲线，
故M的轨迹方程为：
故答案为：
点评：本题考查曲线轨迹方程的求法，圆的几何性质的应用和圆锥曲线的定义是解决问题的关键，属基础题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
，
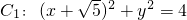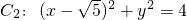中的一个内切，另一个外切．则动圆C的圆心M轨迹L的方程是________．
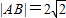，求直线l的方程；
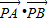，并求
的取值范围．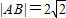
，求直线l的方程；
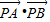，并求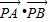
的取值范围．
，
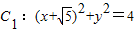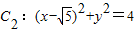中的一个内切，另一个外切．则动圆C的圆心M轨迹L的方程是 ．