题目内容
在△ABC中,cos2
=
,(a,b,c分别为角A,B,C的对边),则△ABC的形状为( )
| B |
| 2 |
| a+c |
| 2c |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
分析:利用二倍角公式代入cos2
=
求得cosB=
,进而利用余弦定理化简整理求得a2+b2=c2,根据勾股定理判断出三角形为直角三角形.
| B |
| 2 |
| a+c |
| 2c |
| a |
| c |
解答:解:∵cos2
=
,∴
=
,∴cosB=
,
∴
=
,
∴a2+c2-b2=2a2,即a2+b2=c2,
∴△ABC为直角三角形.
故选B
| B |
| 2 |
| a+c |
| 2c |
| cosB+1 |
| 2 |
| a+c |
| 2c |
| a |
| c |
∴
| a2+c2-b2 |
| 2ac |
| a |
| c |
∴a2+c2-b2=2a2,即a2+b2=c2,
∴△ABC为直角三角形.
故选B
点评:本题主要考查了三角形的形状判断.考查了学生对余弦定理即变形公式的灵活利用.

练习册系列答案
相关题目
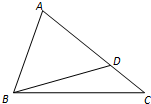 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=