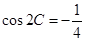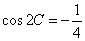Question

(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c，已知

      (I)求sinC的值；

(Ⅱ)当a=2， 2sinA=sinC时，求b及c的长．

Answer 1

解析：本题主要考察三角变换、正弦定理、余弦定理等基础知识，同事考查运算求解能力。

（Ⅰ）解：因为cos2C=1-2sin²C=，及0＜C＜π

所以sinC=.

（Ⅱ）解：当a=2，2sinA=sinC时，由正弦定理，得

c=4

由cos2C=2cos²C-1=，J及0＜C＜π得

cosC=±

由余弦定理c²=a²+b²-2abcosC，得

b²±b-12=0

解得   b=或2

所以   b=            b=

       c=4      或       c=4