题目内容
三棱锥P?ABC中,PA⊥平面ABC,AB⊥BC。

(1)证明:平面PAB⊥平面PBC;
(2)若 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体 的体积。
的体积。

(1)证明:平面PAB⊥平面PBC;
(2)若
 ,
, ,PB与底面ABC成60°角,
,PB与底面ABC成60°角, 分别是
分别是 与
与 的中点,
的中点, 是线段
是线段 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体 的体积。
的体积。试题分析:(Ⅰ)先利用线面垂直的判定定理证明BC⊥平面PAB,再利用面面垂直的判定定理证明平面PAB⊥平面PBC;(2)由已知条件在在
 中,计算可得
中,计算可得 ,可证
,可证 面
面 ,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.
,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.试题解析:17、(1)证明:∵PA^面ABC,\PA^BC,
∵AB^BC,且PA∩AB=A,\BC^面PAB
而BCÌ面PBC中,\面PAB^面PBC. 5分
(2)解:PB与底面ABC成60°角,
即
 , 6分
, 6分在
 中,
中, ,又
,又 ,
,在
 中,
中, 。 8分
。 8分E、F分别是PB与PC的中点,
 面
面 9分
9分 12分
12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
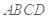 为矩形,
为矩形,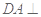 平面
平面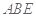 ,
,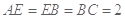 ,
,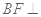 平面
平面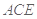 于点
于点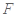 ,且点
,且点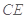 上.
上.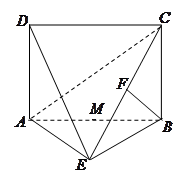
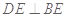 ;
;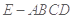 的体积;
的体积;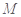 在线段
在线段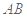 上,且
上,且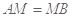 ,试在线段
,试在线段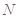 ,使得
,使得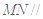 平面
平面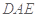 .
. 中,侧棱长均为
中,侧棱长均为 ,底边
,底边 ,
, ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
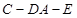 的平面角.
的平面角.
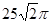

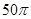
 ,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )
,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )



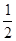 ,则其体积缩小到原来的
,则其体积缩小到原来的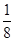 ;
;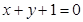 与圆
与圆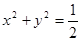 相切.
相切. 倍,则球的半径扩大到原来的 倍,球的体积扩大到原来的 倍.( )
倍,则球的半径扩大到原来的 倍,球的体积扩大到原来的 倍.( ) 、
、
 S2
S2


