题目内容
(本题满分16分)
设数列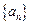 的前
的前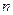 项和为
项和为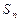 ,若对任意
,若对任意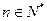 ,都有
,都有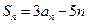 .
.
⑴求数列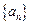 的首项;
的首项;
⑵求证:数列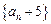 是等比数列,并求数列
是等比数列,并求数列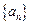 的通项公式;
的通项公式;
⑶数列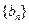 满足
满足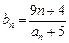 ,问是否存在
,问是否存在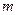 ,使得
,使得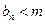 恒成立?如果存在,求出
恒成立?如果存在,求出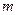 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
设数列
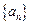 的前
的前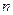 项和为
项和为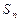 ,若对任意
,若对任意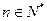 ,都有
,都有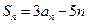 .
.⑴求数列
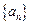 的首项;
的首项;⑵求证:数列
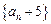 是等比数列,并求数列
是等比数列,并求数列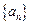 的通项公式;
的通项公式;⑶数列
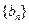 满足
满足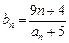 ,问是否存在
,问是否存在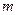 ,使得
,使得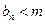 恒成立?如果存在,求出
恒成立?如果存在,求出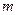 的值,如果不存在,说明理由.
的值,如果不存在,说明理由. ,
,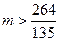
解:
⑴∵
 ∴
∴ ……………………………3分
……………………………3分
⑵∵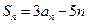 ∴
∴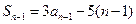 (
(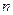 ≥2)
≥2)
∴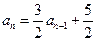 ………………………………5分
………………………………5分
∴

∴ (为常数) (
(为常数) (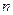 ≥2)
≥2)
∴数列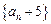 是以
是以 为公比的等比数列 …………………………………7分
为公比的等比数列 …………………………………7分
∴
 …………………………………10分
…………………………………10分
⑶∵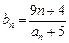 ∴
∴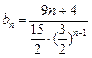
∴ ………………………………12分
………………………………12分
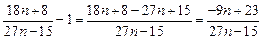 ………………………………14分
………………………………14分
∴当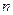 ≥3时,
≥3时, <1; 当
<1; 当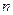 =2时,
=2时, >1
>1
∴当 2时,
2时,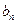 有最大值
有最大值
∴ …………………………………15分
…………………………………15分
∴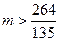
 …………………………………16分
…………………………………16分
⑴∵

 ∴
∴ ……………………………3分
……………………………3分⑵∵
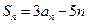 ∴
∴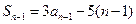 (
(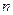 ≥2)
≥2)∴
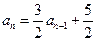 ………………………………5分
………………………………5分∴


∴
 (为常数) (
(为常数) (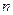 ≥2)
≥2)∴数列
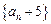 是以
是以 为公比的等比数列 …………………………………7分
为公比的等比数列 …………………………………7分∴

 …………………………………10分
…………………………………10分⑶∵
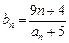 ∴
∴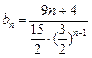
∴
 ………………………………12分
………………………………12分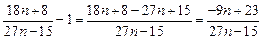 ………………………………14分
………………………………14分∴当
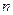 ≥3时,
≥3时, <1; 当
<1; 当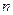 =2时,
=2时, >1
>1∴当
 2时,
2时,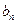 有最大值
有最大值
∴
 …………………………………15分
…………………………………15分∴
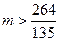
 …………………………………16分
…………………………………16分
练习册系列答案
相关题目
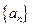 满足
满足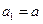 ,
,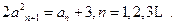
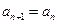 ,求
,求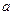 的值;
的值;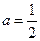 时,证明:
时,证明: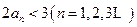 ;
;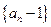 的前
的前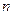 项之积为
项之积为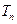 ,若对任意正整数
,若对任意正整数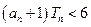 成立,求
成立,求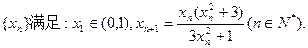
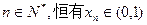 ;
;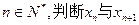 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。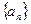 是等差数列,且
是等差数列,且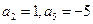
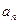 。
。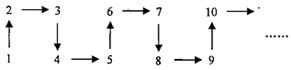
 012箭头的方向是 ( )
012箭头的方向是 ( )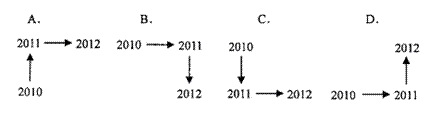
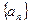 中,
中,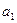 =15,
=15,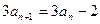 (
(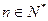 ),则该数列中相邻两项的乘积是负数的是( )
),则该数列中相邻两项的乘积是负数的是( )
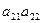
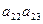
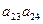
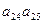
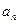 }中,
}中, ,则
,则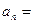 ( )
( )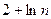
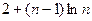
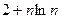
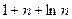
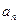 }的前n 项和为
}的前n 项和为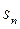 ,已知
,已知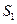 ,
,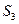 ,
,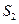 成等差数列
成等差数列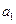 -
-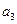 =3,求
=3,求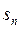
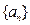 ,
,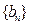 满足
满足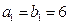 ,
,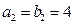 ,
,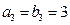 。
。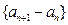 是等差数列,求
是等差数列,求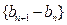 是等比数列,求
是等比数列,求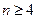 时,
时,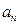 与
与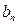 哪一个较大?证明你的结论。
哪一个较大?证明你的结论。