Question

以下四个关于圆锥曲线的命题中：

①双曲线与椭圆有相同的焦点；

②在平面内, 设、为两个定点,为动点,且,其中常数为正实数，则动点的轨迹为椭圆；

③方程的两根可分别作为椭圆和双曲线的离心率；

④过双曲线的右焦点作直线交双曲线于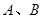两点，若，则这样的直线有且仅有3条。

其中真命题的序号为         （写出所有真命题的序号）．

 

Answer 1

【答案】

①④

【解析】

试题分析：①在双曲线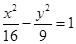中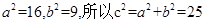，，所以双曲线的的焦点坐标为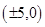，在椭圆中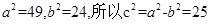，，所以椭圆的焦点坐标为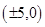，所以它们有相同的焦点，①正确；

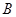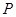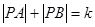②在平面内, 设、为两个定点,为动点,且,其中常数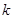为正实数，则动点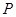的轨迹为椭圆；错误。当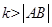，动点P的轨迹是椭圆；当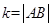时，动点P的轨迹为线段AB；当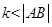时，动点P的轨迹不存在。

③方程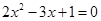的两根可分别作为椭圆和双曲线的离心率，错误，椭圆的离心率在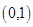内，双曲线的离心率大于1.

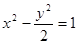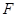④过双曲线的右焦点作直线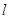交双曲线于两点，若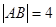，则这样的直线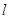有且仅有3条。当垂直x轴时，满足题意；当直线的斜率存在时，设出直线方程可求出另两条。

考点：椭圆的简单性质；双曲线的简单性质；椭圆的定义。

点评：（1）注意椭圆中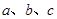的关系式与双曲线中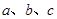的关系式的不同；（2）在平面内，到两定点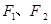的距离和等于常数2a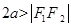（）的点的轨迹为椭圆，当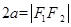时，点的轨迹为线段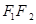；当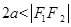时，点的轨迹不存在。