Question

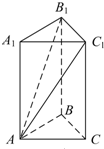（2013•成都模拟）如图，在三棱柱ABC-A₁B₁C₁中，侧棱垂直于底面，底面是边长为2的正三角形，侧棱长为3，则BB₁与平面AB₁C₁所成的角是（　　）

• A．

  π

  6

• B．

  π

  4

• C．

  π

  3

• D．

  π

  2

Answer 1

分析：以B为坐标原点，建立空间直角坐标系，利用

BB1

与平面AB₁C₁所的一个法向量 的夹角，求出则BB₁与平面AB₁C₁所成的角．

解答：解：以B为坐标原点，以与BC垂直的直线为x轴，BC为y轴，建立空间直角坐标系，
则A（

3

，1，0），B₁（0，0，3），C₁（0，2，3），

AB1

=（-

3

，-1，3），

B1C1

=（0，2，0），

BB1

=（0，0，3）．
设平面AB₁C₁所的一个法向量为

n

=（x，y，z）
则

AB1 • n =0 B1C1 • n =0

即

- 3 x-y+3z=0 2y=0

，取z=1，则得

n

=（-

3

，0，1），
∵cos＜

BB1

，

n

＞=

BB1 • n

| BB1 || n |

=

3

3× 2

=

1

2

，
∴BB₁与平面AB₁C₁所成的角的正弦值为

1

2

，
∴BB₁与平面AB₁C₁所成的角为

π

6

 
故选A．

点评：本题考查线面角的计算，利用了空间向量的方法．要注意相关点和向量坐标的准确性，及转化时角的相等或互余关系．