题目内容
对函数f (x),若 ,f (a), f (b), f (c)为一三角形的三边长,则称f (x)为“三角型函数”,已知函数
,f (a), f (b), f (c)为一三角形的三边长,则称f (x)为“三角型函数”,已知函数 是“三角型函数”,则实数m 的取值范围是( )
是“三角型函数”,则实数m 的取值范围是( )
| A.[1, 4] | B.[0,2] | C.[ 2, 4] | D.[1, 2 ] |
A
解析试题分析:由题意可得,f(a)+f(b)>f(c)对任意的a、b、c∈R恒成立,∵函数 ,∴当m≥2时,函数f(x)在R上是减函数,函数的值域为
,∴当m≥2时,函数f(x)在R上是减函数,函数的值域为 ;故f(a)+f(b)>2,f(c)<
;故f(a)+f(b)>2,f(c)< ,∴m≤4 ①.当m<2时,函数f(x)在R上是增函数,函数的值域为(
,∴m≤4 ①.当m<2时,函数f(x)在R上是增函数,函数的值域为( ,1);故f(a)+f(b)>m,f(c)<1,∴m≥1,②.由①②可得1≤m≤4,故选:A.
,1);故f(a)+f(b)>m,f(c)<1,∴m≥1,②.由①②可得1≤m≤4,故选:A.
考点:函数的值.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知函数 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数f(n)=  ,其中n∈N,则f(8)等于( )
,其中n∈N,则f(8)等于( )
| A.2 | B.4 | C.6 | D.7 |
函数 的值域是( )
的值域是( )
A. | B. |
C. | D. |
已知函数 ,
, ,则
,则 的值为
的值为
| A.2 | B.-2 | C.6 | D.-6 |
函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当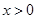 时,
时, ,则
,则 ( )
( )
| A.1 | B.-1 | C.2 | D.-2 |
下列幂函数中过点 ,
, 的偶函数是( )
的偶函数是( )
A. | B. | C. | D. |
 的图像不经过第四象限,则函数
的图像不经过第四象限,则函数 的值域为
的值域为  ,若f(1)=2,则f(107)=__________.
,若f(1)=2,则f(107)=__________.