题目内容
已知偶函数f（x）在区间[0，+∞）上单调增加，则满足f（2x-1）＜f（
）的x取值范围是________．
（，
）
分析：本题采用画图的形式解题比较直观．
解答：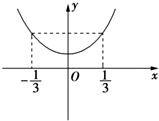
解：如图所示：
∵f（2x-1）＜f（）
∴-＜2x-1＜，
即＜x＜．
故答案为：（，）
点评：本题考查函数的奇偶性的应用．关键是利用了偶函数关于y轴对称的性质．
，）分析：本题采用画图的形式解题比较直观．
解答：
解：如图所示：∵f（2x-1）＜f（
）∴-
＜2x-1＜，即
＜x＜．故答案为：（
，）点评：本题考查函数的奇偶性的应用．关键是利用了偶函数关于y轴对称的性质．
练习册系列答案
相关题目
已知偶函数f（x）在区间[0，π]上单调递增，那么下列关系成立的是（ ）
A、f(-π)＞f(-2)＞f(
| ||
B、f(-π)＞f(-
| ||
C、f(-2)＞f(-
| ||
D、f(-
|