题目内容
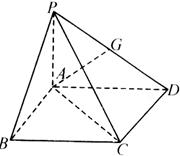
如图,在四棱锥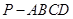 中,
中,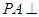 平面
平面 四边形
四边形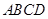 为正方形,
为正方形,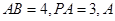 点在
点在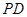 上的射影为
上的射影为 点.
点.
(1)求证: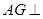 平面
平面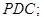
(2)在棱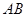 上是否存在一点
上是否存在一点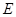 ,使得
,使得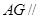 平面
平面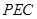 .若存在,求出
.若存在,求出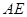 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】
(1)见解析 (2)  .
.
【解析】(1)由已知得 ,要证
,要证 平面
平面 ,关键是证
,关键是证 ,由已知易证出
,由已知易证出 ,结论得证;(2)假设存在一点
,结论得证;(2)假设存在一点 ,使得
,使得 平面
平面 ,再作
,再作 ,得到面面平行,根据面面平行的性质定理得线线平行,把要求的
,得到面面平行,根据面面平行的性质定理得线线平行,把要求的 转化为求
转化为求 利用三角形相似,对应线段成比例计算得
利用三角形相似,对应线段成比例计算得 的值。
的值。
(1)
 又
又


 又
又

(2)假设棱 存在一点
存在一点 ,使
,使 .过
.过 作
作 ,连
,连 ,则
,则 ,
,
 它们都与平面
它们都与平面 相交,
相交,


 设
设 ,则
,则 在
在 ,可求
,可求
 即
即 ,
, 因此存在点
因此存在点 满足题意,
满足题意,

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.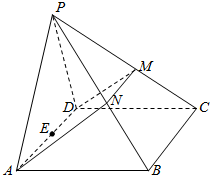 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥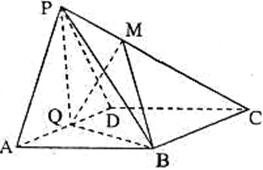 试确定
试确定