题目内容
设双曲线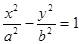 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x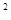 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ).
A.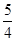 | B.5 | C.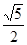 | D.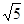 |
D
解析试题分析:
先根据双曲线方程表示出渐近线方程与抛物线方程联立,利用判别式等于0求得a和b的关系,进而求得a和c的关系,则双曲线的离心率可得.解:因为依题意可知双曲线渐近线方程为 ,与抛物线方程联立消去y得
,与抛物线方程联立消去y得
故可知选D.
考点:双曲线方程以及性质
点评:本题主要考查了双曲线的简单性质和圆锥曲线之间位置关系.常需要把曲线方程联立根据判别式和曲线交点之间的关系来解决问题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线x2=-y,的准线方程是( )。
A. | B. | C. | D. |
设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为( ).
,则双曲线的渐近线方程为( ).
A.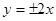 | B. | C.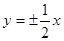 | D. |
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
从抛物线 上任意一点
上任意一点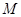 向圆
向圆 作切线
作切线 ,则切线长
,则切线长 的最小值为
的最小值为
A.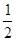 | B.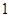 | C. | D.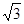 |
抛物线 的焦点为F,倾斜角为
的焦点为F,倾斜角为 的直线
的直线 过点F且与抛物线的一个交点为A,
过点F且与抛物线的一个交点为A, ,则抛物线的方程为
,则抛物线的方程为
A. | B. |
C. 或 或 | D. 或 或 |
双曲线
 的两个焦点为
的两个焦点为 、
、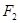 ,双曲线上一点
,双曲线上一点 到
到 的距离为12,则
的距离为12,则 到
到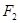 的距离为( )
的距离为( )
| A.17 | B.22 | C.7或17 | D.2或22 |
已知椭圆 的上、下顶点分别为
的上、下顶点分别为 、
、 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,若四边形
,若四边形 是正方形,则此椭圆的离心率
是正方形,则此椭圆的离心率 等于
等于
A. | B. | C. | D. |
 的一条渐近线与圆
的一条渐近线与圆 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )


